Теорема. Пусть дан интеграл  ,где
,где  непрерывна на
непрерывна на  . Введем новую переменную
. Введем новую переменную  , связанную с
, связанную с  равенством
равенством  . Если
. Если
1)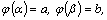
2)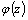 и
и  непрерывны на
непрерывны на  ,
,
3)при изменении  от α до β значения
от α до β значения 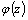 не выходят за пределы отрезка
не выходят за пределы отрезка  то
то 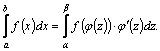
Доказательство. Пусть  –первообразная для функции
–первообразная для функции  ,то есть
,то есть  . Тогда по формуле Ньютона–Лейбница
. Тогда по формуле Ньютона–Лейбница
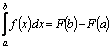
Покажем, что функция  является первообразной для функции
является первообразной для функции  *
*  = [по правилу дифференцирования сложной функции] =
= [по правилу дифференцирования сложной функции] = Тогда по формуле Ньютона–Лейбница
Тогда по формуле Ньютона–Лейбница
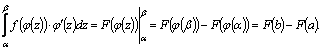
Сравнивая равенства (I) и (II), убеждаемся в справедливости формулы (5)