ПРЕДИКАТЫ
1. Придумать два предиката 
и 
на множестве 
, что предикат
a. 
– тождественно - ложный, но каждый из предикатов и не является тождественно - ложным;
b. 
– тождественно - истинный, но каждый из предикатов и не является тождественно - истинным;
c. 
– тождественно - ложный и один из предикатов и есть отрицание другого.
2. Даны некоторые предикаты и на множестве 
. Для следующих предикатов найти им равносильные, не содержащие кванторов:
a. 
;
b. 
;
c. 
;
d.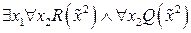 
;
e.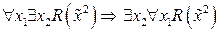 
;
f. 
.
3. Найти значение высказывания 
, где предикат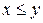 
на множестве: 1) натуральных чисел; 2) целых чисел, и значения следующих высказываний, образованных из предикатов на множестве целых чисел:
a. 
;
b. 
;
c. 
;
d.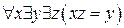 
;
e. 
;
f.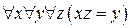 
;
g. 
.
4. Записать на языке предикатов следующие высказывания:
a. каждое положительное действительное число является квадратом другого;
b. натуральное число, которое делится на 9, разделится на 3;
c. две прямые, параллельные третьей, параллельны между собой;
d. если две прямые на плоскости не параллельны, то они имеют общую точку, притом только одну;
e. через две различные точки плоскости проходит прямая и только одна;
f. каждый предикат является тождественно-ложным или выполнимым;
g. над одним предикатом может быть выполнена только одна из операций: 
, 
, 
.
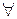h. над некоторым предикатом некоторые операции дают высказывания.
