1 - 20. Даны векторы а (а1 ; а2 ; а3 ), b (b1 ; b2 ; b3 ), с (с1 ; с2 ; с3 ) и d (d1 ; d2 ; d3 ) в некотором базисе. Показать, что векторы а , b , c образуют базис, и найти координаты вектора d в этом базисе.
1. а (1;2;3), b (-1;3;2), с (7;-3;5), d (6;10;17).
2. а (4;7;8), b (9;1;3), с (2;-4;1), d (1;-13;-13).
3. а (8;2;3), b (4;6;10), с (3;-2;1), d (7;4;11).
4. а (10;3;1), b (1;4;2), с (3;9;2), d (19;30;7).
5. а (2;4;1), b (1;3;6), с (5;3;1), d (24;20;6).
6. а (1;7;3), b (3;4;2), с (4;8;5), d (7;32;14).
7. а (1;-2;3), b (4;7;2), с (6;4;2), d (14;18;6).
8. а (1;4;3), b (6;8;5), с (3;1;4), d (21;18;33).
9. а (2;7;3), b (3;1;8), c (2;-7;4), d (16;14;27).
10. а (7;2;1), b (4;3;5), с (3;4;-2), d (2;-5;-13)
11. а (4;1;0) b (0; 1; -2) с (3;-1;1), d (-5; 9; -13)
12. а (-1;1;0)b (0; 5; 1) с (3;2;-1), d (-15; 5; 6)
13. а (1;3;0) b (1; 0; 1) с (0;-2;1), d (8; 9; 4)
14. а (2; 1; 0) b (1; -1; 0) с (-3;2;5), d (23; -14; -30)
15. а (2; 1; 0) b (1; 0; 1) с (4;2;1), d (3; 1; 3)
16. а (0; 3; 1) b (1; -1; 2) с (2;-1;0), d (-1; 7; 0)
17. а (1; -1; 2) b (3; 2; 0) с (-1;1;1), d (11; -1; 4)
18. а (1; 1; 4) b (-3; 0; 2) с (1;2;-1), d (-13; 2; 18)
19. а (0; -2; 1) b (3; 1; -1) с (4;0;1), d (0; -8; 9)
20. а (0; 1; 5) b (3; -1; 2) с (-1;0;1), d (8; -7; -13)
21 - 40. Даны координаты вершин пирамиды А1 А2 А3 А4 . Найти 1) длину ребра А1 А2 ; 2) угол между ребром А1 А2 и А1 А4 ; 3) угол между ребрами А1 А4 и гранью А1 А2 А3 ; 4)площадь грани А1 А2 А3 ; 5) объем пирамиды; 6) уравнение прямой А1 А2 ; 7) уравнение плоскости А1 А2 А3 ; 8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3 . Сделать чертеж.
21. А1 (4;2;5), А2 (0;7;2), А3 (0;2;7), А4 (1;5;0).
22 . А1 (4;4;10), А2 (4;10;2), А3 (2;8;4), А4 (9;6;4).
23. А1 (4;6;5), А2 (6;9;4), А3 (2;10;10), А4 (7;5;9).
24. А1 (3;5;4), А2 (8;7;4), А3 (5;10;4), А4 (4;7;8).
25. А1 (10;6;6), А2 (-2;8;2), А3 (6;8;9), А4 (7;10;3).
26. А1 (1;8;2), А2 (5;2;6), А3 (5;7;4), А4 (4;10;9).
27. А1 (6;6;5), А2 (4;9;5), А3 (4;6;11), А4 (6;9;3).
28. А1 (7;2;2), А2 (5;7;7), А3 (5;3;1), А4 (2;3;7).
29. А1 (8;6;4), А2 (10;5;5), А3 (5;6;8), А4 (8;10;7).
30. А1 (7;7;3), А2 (6;5;8), А3 (3;5;8), А4 (8;4;1).
31. А1 (1;3;6), А2 (2;2;1), А3 (-1;0;1), А4 (-4;6;-3).
32. А1 (-4;2;6), А2 (2;-3;0), А3 (-10;5;8), А4 (-5;2;-4).
33. А1 (7;2;4), А2 (7;-1;-2), А3 (3;3;1), А4 (-4;2;1).
34. А1 (2;1;4), А2 (-1;5;-2), А3 (-7;-3;2), А4 (-6;-3;6).
35. А1 (-1;-5;2), А2 (-6;0;-3), А3 (3;6;-3), А4 (-10;6;7).
36 . А1 (0;-1;-1), А2 (-2;3;5), А3 (1;-5;-9), А4 (-1;-6;3).
37. А1 (5;2;0), А2 (2;5;0), А3 (1;2;4), А4 (-1;1;1).
38. А1 (2;-1;-2), А2 (1;2;1), А3 (5;0;-6), А4 (-10;9;-7).
39. А1 (-2;0;-4), А2 (-1;7;1), А3 (4;-8;-4), А4 (1;-4;6).
40. А1 (14;4;5), А2 (-5;-3;2), А3 (-2;-6;-3), А4 (-2;2;-1).
41 - 60. Дана система линейных уравнений:
Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) методом Крамера.
41. 42.
43. 44.
45. 46.
47. 48.
49. 50.
51. 52.
53. 54.
55. 56.
57. 58.
59. 60.
61 - 80. Найти пределы функций, не пользуясь правилом Лопиталя.
61.
а) б) в) г)
62.
а) б) в) г) 63.
а) б) в) г) 64.
а) б) в) г) 65.
а) б) в) г) 66.
а) б) в) г) 67.
а) б) в) г) 68.
а) б) в) г) 69.
а) б) в) г) 70.
а) б) в) г) 71.
а) б) в) г) 72.
а) б) в) г) 73.
а) б) в) г)
а) б) в) г) 75.
а) б) в) г) 76.
а) б) в) г) 77.
а) б) в) г) 78.
а) б) в) г) 79.
а) б) в) г) 80.
а) б) в) г)
81 – 100. Найти производные
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101 - 120. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
101. у = 4х/(4+х2 ) 102. y = (x2 -1)/(x2 +1)
103. y = (x2 +1)/(x2 -1) 104. y = x2 /(x-1)
105 . y = x3 /(x2 +1) 106. y = (4x3 +5)/x
107. y = (x2 -5)/(x-3) 108. y = x4 /(x3 -1)
109. y = 4x3 /(x3 -1) 110. y = (2-4x2 )/(1-4x2 )
111. y = (1nx)/ 112 . y = x
113. y = 114. y = x2 -21nx
115. y = 1n (x2 -4) 116. y = e1/(2-x)
117. y = 1n (x2 +1) 118. y = (2+x2 )
119. y = 1n (9-x2 ) 120. y = (x-1)e3x+1 .
121 - 140. Найти неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141. Вычислить площадь фигуры, ограниченной параболой у = 3х2 + 1 и
прямой у = 3х + 7 .
142. Вычислить площадь фигуры, ограниченной одной аркой циклоды
х = а(t - sin t), y = a(1 - cos t),
143. Вычислить площадь фигуры, ограниченной кардиоидой
r = 3(1 + cos φ).
144. Вычислить площадь фигуры, ограниченной четырехлепестковой розой
r = 4sin 2φ .
145. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами у = х2 и у =
146. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом у = х = и осью Оу.
147. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2/(1 + х2 )4 и у = х2 .
148. Вычислить длину дуги полукубической параболы у = от точки А (2;0) до точки В (6;8).
149. Вычислить длину кардиоиды r = 3(1 - cosφ).
150. Вычислить длину одной арки циклоиды х = 3(t - sint), y = 3(1 - cost),
151. Вычислить длину дуги
152. . Вычислить объем тела, образованного вращением фигуры, ограниченных графиками функций
153. Вычислить площадь фигуры, ограниченной графиками функций.
154. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями.
155. Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах.
156. . Вычислить длину дуги кривой, заданной параметрическими уравнениями
157. . Вычислить длину дуги кривой, заданной уравнениями в полярных координатах
158. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций
159. Вычислить длину дуги
160. Вычислить длину дуги


 42.
42. 
 44.
44. 
 46.
46. 
 48.
48. 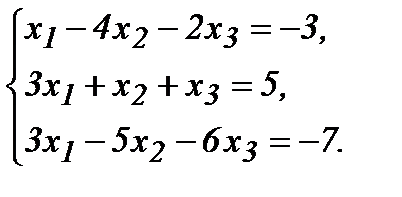
 50.
50. 
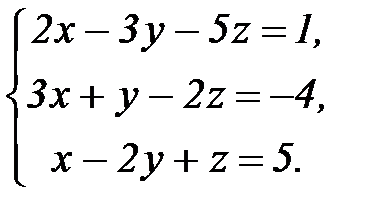 52.
52. 
 54.
54. 
 56.
56. 
 58.
58. 
 60.
60. 









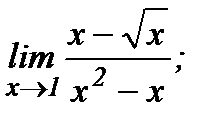






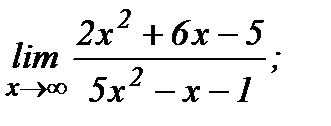















































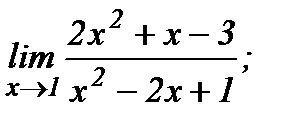















 данных функций.
данных функций.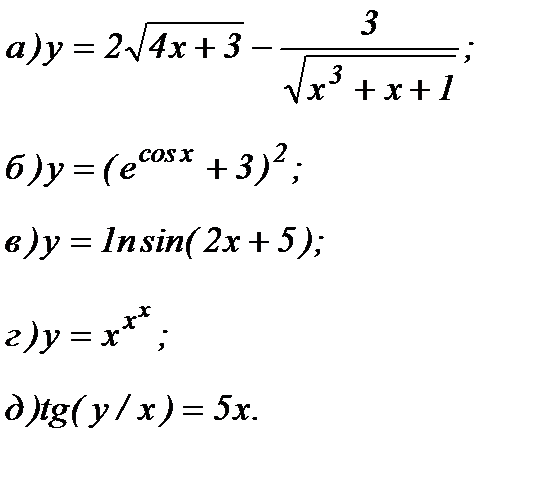
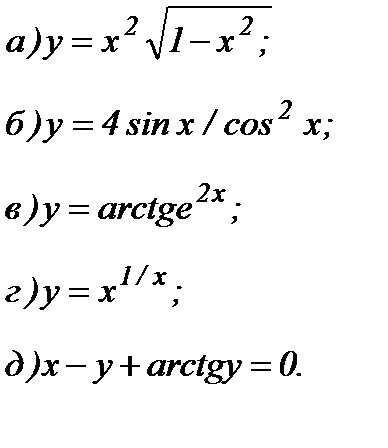


















 112. y = x
112. y = x 
 114. y = x2-21nx
114. y = x2-21nx













 ;
;


 ;
;



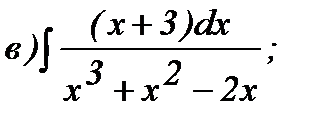

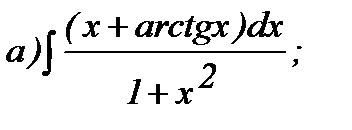














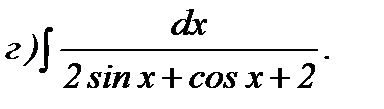




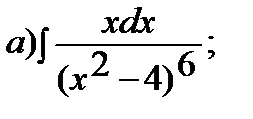










 ;
;
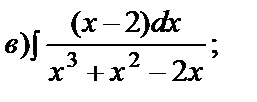
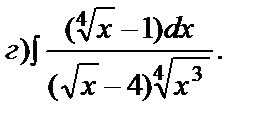















 и осью Ох.
и осью Ох. .
. , параболой х =
, параболой х =  и осью Оу.
и осью Оу. от точки А (2;0) до точки В (6;8).
от точки А (2;0) до точки В (6;8). .
.
 . Ось вращения
. Ось вращения 



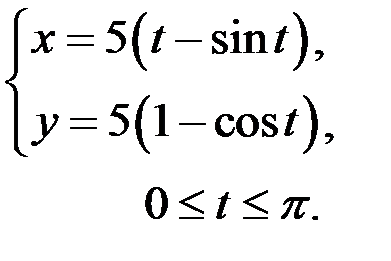

 . Ось вращения
. Ось вращения 
