Пусть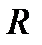 
– произвольная ДНФ, которую можно представить следующим образом:
, 
.
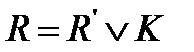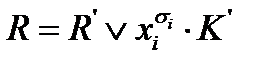Здесь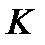 
– элементарная конъюнкция из 
, 
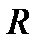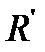– ДНФ, образованная из остальных конъюнкций, входящих в 
; 
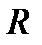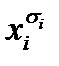– некоторый множитель из ; 
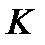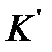– произведение остальных множителей из .
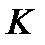Рассмотрим два типа преобразования ДНФ.
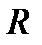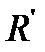I. Операция удаления элементарной конъюнкции. Переход от ДНФ к ДНФ – преобразование, осуществляемое путем удаления элементарной конъюнкция 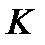. Данное преобразование определено тогда и только тогда, когда 
.
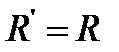II. Операция удаления множителя. Переход от 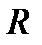ДНФ к ДНФ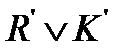 
– преобразование, осуществляемое путем удаления множителя 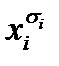. Данное преобразование определено тогда и только тогда, когда 
.
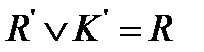ДНФ 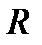, которую нельзя упростить при помощи преобразований I и II, называется тупиковой ДНФ. (ТДНФ).
Например, очевидно, что ДНФ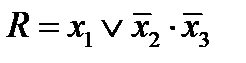 
будет тупиковой.
