Обозначим через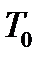 
класс всех булевых функций 
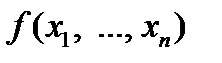из 
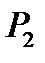, сохраняющих константу 0, то есть функций, которые равны нулю на нулевом наборе переменных:
.
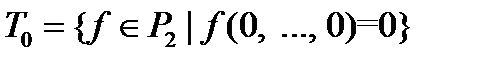Заметим, что если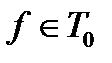 
, а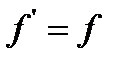 
, то и 
.
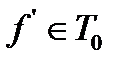Легко убедиться, что функции 0,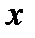 
, 
, 
, 
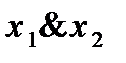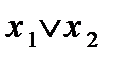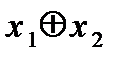принадлежат классу 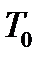, а функции 1, 
, 
, 
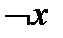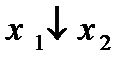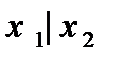не входят в .
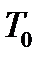Поскольку таблица для функции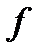 
из класса 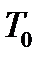в первой строке содержит значение 0, то в 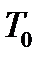содержится ровно 
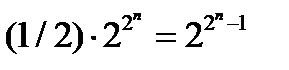булевых функций от 
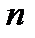переменных.
Покажем, что 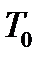– замкнутый класс. Для этого надо доказать следующее утверждение.
Лемма 1. Суперпозиция функций из класса 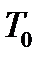является функцией класса .
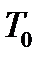Для доказательства необходимо убедиться, что применение операци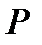й 
и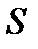 
к функциям, сохраняющим 0, всякий раз дает функцию, сохраняющую 0.
В результате операции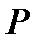 
для функции 
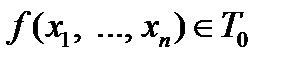имеем формулу 
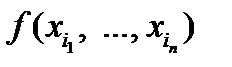, которая при нулевых значениях своих аргументов совпадает с 
.
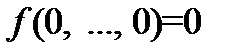Теперь покажем, что функция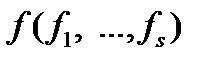 
, полученная в результате применения операции 
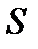, принадлежит 
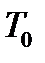, если 
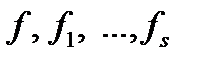принадлежат :
.
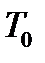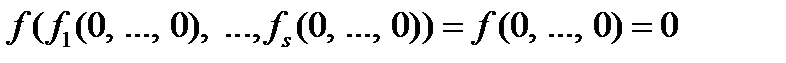Лемма доказана.
Пример 1.Функци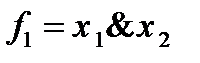и 
и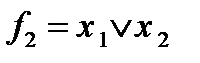 
входят в 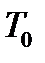, поэтому суперпозиция этих функций будет сохранять 0. Следовательно, система 
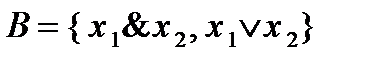неполная.
