Т.к. y’ сама является функцией, то естественно поставить вопрос о наличии ее производной, т.е. (y’)’. Все это можно обобщить определением:
производная от производной порядка n-1 называется производной порядка n.
Соответственно записывают символ такой производной y(n)=(y(n-1))’. Если использовать для обозначения символ дифференциала, то получим иные обозначения производной порядка n. y(n)= 
= 
= 
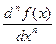и т.д. В самом деле по определению имеем y’’=(y’)’=(f’(x)dx)’=(f’’(x)dx)dx=f’’(x)d2x. Откуда и получаем в виде обобщения записанное ранее.
Из этого определения вытекают и все свойства такой производной.
Рассмотрим несколько частных случаев производной порядка n.
Пусть y=uv. Тогда y’=u’v+v’u. Затем y’’=u’’v+2u’v’+v’’u. Обобщаем и получаем
(uv)(n) =u(n) v+n u(n-1) v’+ 
+…+ uv(n) . коэффициенты такой формулы можно сразу выписать, если использовать треугольник Паскаля.
Пусть функция задана параметрически 
. Тогда известно, что y’= 
. Если теперь попытаться найти y’’, то сделать это будет проблематично, т.к. получено выражение, зависящее от t ,но не от х. Обойдем это затруднение так – имеем
y’’=(y’)’= 
y’= ( )= 
= 
= 
= 
.
Можно поступить иначе
y’’=(y’)’= y’= ( )= ( 
)= 
= 
.
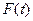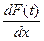