Формулы сложения
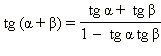
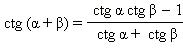cos (α + β) = cos α cos β – sin α sin β
cos (α – β) = cos α cos β + sin α sin β
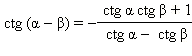
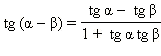sin (α + β) = sin α cos β + cos α sin β
sin (α – β) = sin α cos β – cos α sin β
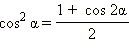Формулы понижения степени
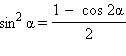
Формулы двойных и кратных углов
sin 2α = 2 sin α cos α
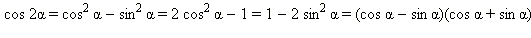
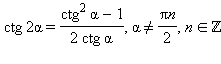
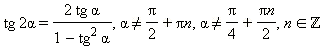
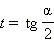
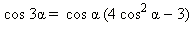
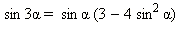
Универсальная замена
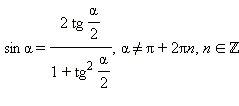
Формулы половинного аргумента
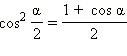
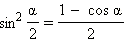
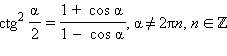
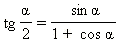
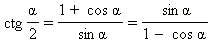
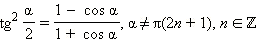
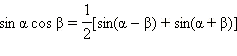
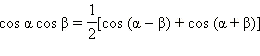Преобразование произведения в сумму
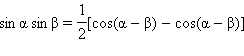
Частные случаи тригонометрических уровнений
· Уравнение sin x = a
x = ( —1)n arcsin a + πn, n ∈ Z.
Частные случаи:
1. sin x = 0 ⇒ x = πn, n ∈ Z.
2. sin x = 1 ⇒ x = π/2 + 2πn, n ∈ Z.
3. sin x = -1 ⇒ x = -π/2 + 2πn, n ∈ Z.
· Уравнение tg x = a
x = arctg a + πn, n ∈ Z.
· cos x = a
x = ±arccos a + πn, n ∈ Z.
Частные случаи:
1. cos x = 0 ⇒ x = π/2 + πn, n ∈ Z.
2. cos x = 1 ⇒ x = 2πn, n ∈ Z.
3. cos x = -1 ⇒ x = π + 2πn, n ∈ Z.
· Уравнение ctg x = a
x = arcctg a + πn, n ∈ Z
