Рассмотрим два произвольных ненулевых вектора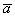 
и 
:
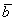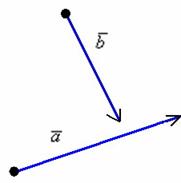
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 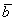от конца вектора :
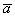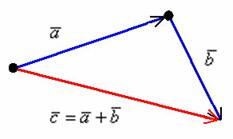
Суммой векторов 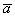и 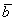является вектор 
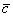. Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору 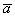, а затем по вектору 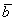. Тогда сумма векторов 
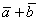представляет собой вектор результирующего пути 
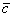с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
Кстати, если вектор 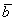отложить от начала вектора 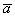, то получится эквивалентное правило параллелограмма сложения векторов.
