Вычисление энтропии систем

Проверка

Считаем, что вектор рассчитан верно, если сумма его элементов равна единице. Это утверждение справедливо и для матрицы P(A,B). В случае матриц P(a_i/b_j)/P(b_j/a_i), единице должна равняться сумма каждого столбца/строки матрицы.

Проверка вектора P(a):

0.19 + 0.39 + 0.42 = 1.00.

Проверка вектора P(b):

0.25 + 0.27 + 0.48= 1.00.

Проверка матрицы P(A,B):

0.16 + 0.01 + 0.02 + 0.04+0.26+ 0.09 + 0.05+ 0 + 0.37 = 1.00.

Проверка матрицы P(a_i/b_j):

0.64 + 0.16 + 0.2 = 1.000;

0.037 + 0.963 + 0.000 = 1.000;

0.042 + 0.188 + 0.771 = 1.001.

Проверка матрицы P(b_j/a_i):

0.842 + 0.053 + 0.105 = 1.000;

0.103 + 0.667 + 0.231= 1.001;

0.119 + 0.000 + 0.881 = 1.000.

Погрешность вычислений:

.

Вычисление энтропии систем

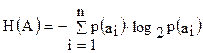; (6)

, (7)

где H(A) — энтропия системы А в сложной системе;

H(B) — энтропия системы B в сложной системе;

P(a_i) — вероятности появления события a_i;

P(b_j) — вероятности появления события b_j.

Зная вероятности p(a_i) и формулу (6), вычислим энтропию системы А:

H(A) =-(0.19 * log₂ (0.19) + 0.39 * log₂(0.39) + 0.42 *log₂ (0.42))=

= 0.4552 +0.5298+0.5256 = 1.5106 (бит/символ).

Зная вероятности p(b_j) и формулу (7), вычислим энтропию системы B:

H(B) = -(0.25 * log₂ (0.25) + 0.27 * log₂ (0.27) +0.48*log₂ (0.48)) = = 0.5000+0.5100+0.5083 = 1.5183 (бит/символ).