Дифференциальное уравнение (д.у.)
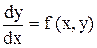
Называется однородным д.у. относительно  и
и 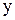 , если функция
, если функция 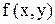 является однородной функцией своих аргументов нулевого измерения. Это значит
является однородной функцией своих аргументов нулевого измерения. Это значит
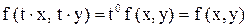 . Например функция
. Например функция 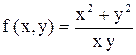 - однородная
- однородная
функция нулевого измерения.
Однородное д.у. всегда можно представить в виде
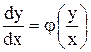 (1)
(1)
Введя новую искомую функцию 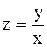 , уравнение (1) можно привести к уравнению с разделяющимися переменными:
, уравнение (1) можно привести к уравнению с разделяющимися переменными: 
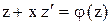 или
или 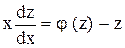 переменные разделяются.
переменные разделяются.
Пример 3.
Решить уравнение 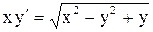 .
.
Решение. Запишем уравнение в виде 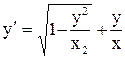 , разделив на
, разделив на  обе части уравнения. Сделаем замену
обе части уравнения. Сделаем замену 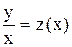 . Тогда
. Тогда 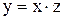 ,
, 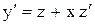 . Получим
. Получим 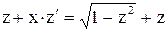 или
или 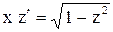 .
.
Разделяя переменные, будем иметь 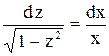 .
.
Отсюда интегрированием находим
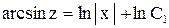
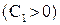 или
или
 , так как
, так как 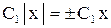 , то обозначая
, то обозначая 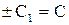 , получим
, получим
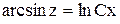 . Заменяя
. Заменяя 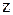 на
на  , будем иметь общий интеграл
, будем иметь общий интеграл
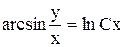 , отсюда
, отсюда 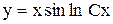 - общее решение.
- общее решение.
Ответ: 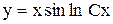 .
.
Упражнения. Решить уравнения
1. 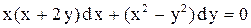 . Ответ:
. Ответ: 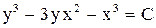 .
.
2. 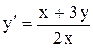 . Ответ:
. Ответ: 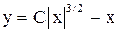 .
.
3.  . Ответ:
. Ответ: 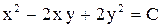 .
.
4.  . Соберем коэффициенты при
. Соберем коэффициенты при 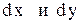
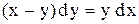 . Ответ:
. Ответ: 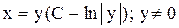 .
.
Решить однородные дифференциальные уравнения.
| 1.
| 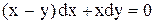 . .
|
| 2.
| 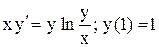 . .
|
| 3.
|  . .
|
| 4.
| 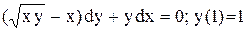 . .
|
| 5.
| 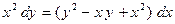 . .
|
| 6.
| 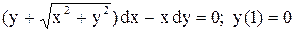 . .
|
| 7.
| 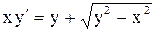 . .
|
| 8.
| 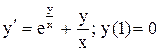 . .
|
| 9.
| 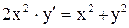 . .
|
| 10.
|  . .
|
| 11.
| 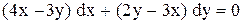 . .
|
| 12.
| 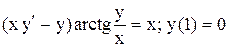 . .
|
| 13.
| 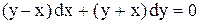 . .
|
| 14.
| 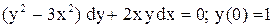 . .
|
| 15.
|  . .
|
| 16.
| 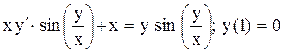 . .
|
| 17.
| 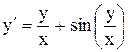 . .
|
| 18.
| 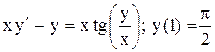 . .
|
| 19.
| 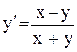 . .
|
| 20.
| 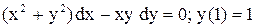 . .
|
| 21.
| 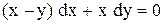 . .
|
| 22.
| 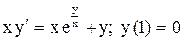 . .
|
| 23.
|  . .
|
| 24.
| 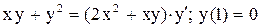 . .
|
| 25.
| 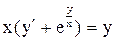 . .
|
| 26.
| 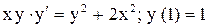 . .
|
| 27.
| 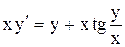 . .
|
| 28.
| 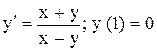 . .
|
| 29.
| 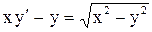 . .
|
| 30.
| 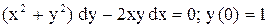 . .
|