1.) Каноническое уравнение прямой
L:  (1)
(1)
M0 (x0;y0;z0) - любая точка на прямой L .
l, m, n – проекции направляющего вектора прямой L на оси Ox, Oy, Oz соответственно. Хотя бы одно из чисел l, m, n отлично от нуля.
2). Уравнение прямой, проходящей через две заданные точки M1 (x1 ,y1 , z1 ) и M2 (x2 ,y2 , z2),
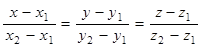 (2)
(2)
где (x 1,y 1 ,z 1) - координаты одной точки на прямой, (x2 ,y2 ,z 2) - координаты другой точки на прямой, (x,y,z) - координаты любой точки на прямой.
3.) Параметрическое уравнение прямой
 (3)
(3)
M0 (x0;y0;z0) - любая точка на прямой, l, m, n – проекции направляющего вектора прямой, t – параметр, изменяя который можно получить все точки прямой.
4.) Условие параллельности прямых