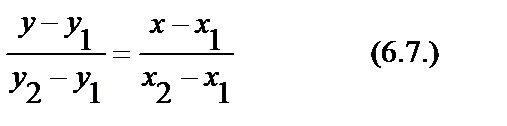Пусть на плоскости дана прямоугольная декартовая система координат и некоторая прямая
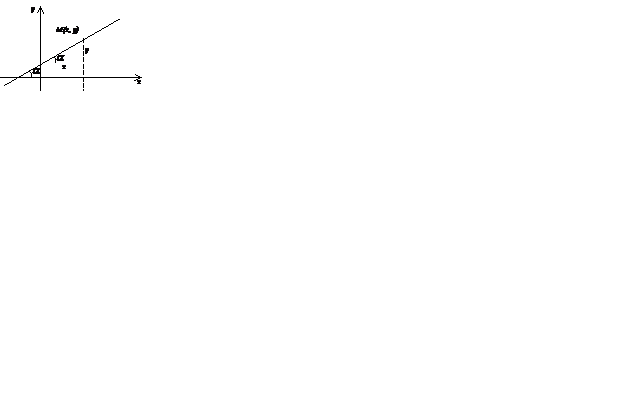
Рис.6.1.
В качестве параметра характеризующего положение на плоскости невертикальной прямой берут величину тангенса угла aмежду прямой и осью Ox.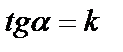 
— угловой коэффициент или тангенс угла наклона прямой к оси 0x.
Если даны две точки прямой 
и 
, то угловой коэффициент определяется формулой 
.
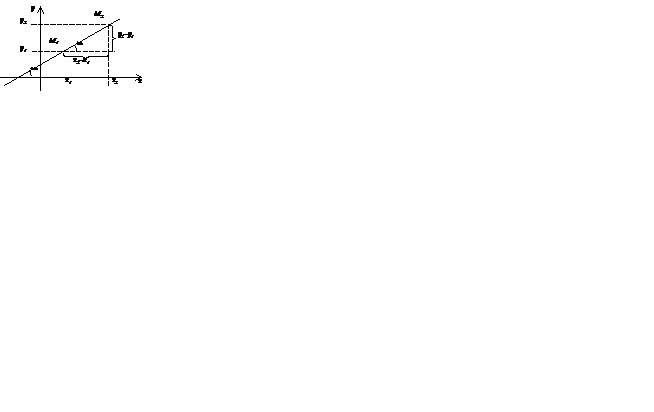
Рис.6.2.
Уравнение y=kx+b (6.1.) называется уравнением прямой с угловым коэффициентом.
Всякое уравнение первой степени относительно x и y определяет на плоскости прямую.
, (6.2.)
, 
.
Задача 6.1. Написать уравнение прямой с угловым коэффициентом k, проходящий через данную точку 
.
Решение: Запишем уравнение (6.1.), т.к. прямая проходит через т. 
ее координаты удовлетворяют уравнению (6.1.) , получим
(6.3.)
Вычтем из уравнения (6.1.) уравнение (6.3.) получим искомое уравнение: 
(6.4.)
Задача 6.2. Написать уравнение прямой проходящей через заданные точки 
, 
.
Решение: Пусть прямая проходит через т.M1, ее координаты удовлетворяют уравнению (6.4.)
. (6.5.)
Прямая проходит через т. 
, следовательно ее координаты также удовлетворяют уравнению (6.5.), т.е. выполняется равенство:
(6.6.)
Разделим (6.5.) на (6.6.) получим искомое уравнение: 
