Определение 1.7.1.
Матрица А-1nxn называется обратной к матрице Аnxn , если А-1×А = А×А-1 =I
Где I единичная матрица порядка n
Обратная матрица существует только для квадратных матриц . Однако не каждая квадратная матрица имеет обратную . Матрица для которой существует обратная называется обратимой . Найдем условия обратимости.
Определение 1.7.2.
Матрица Аnxn называется вырожденной , если ее определитель равен нулю и невырожденной, если определитель не равен нулю.
Определение 1.7.3.
Матрица вида
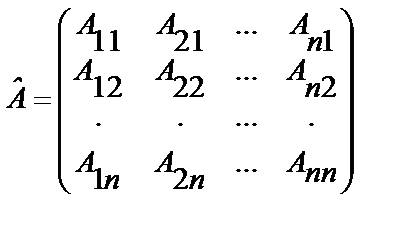
где Aij алгебраические дополнения элемента аij матрицы А, называется присоединенной или союзной матрицей к матрице A .
Сформулируем критерии обратимости матрицы :
Теорема 1.7.1. Матрица Аnxn обратима тогда и только тогда когда она не вырождена т.е. А-1$Ы¦А¦№ 0
Доказательство:
Необходимость 
то по определению 
(по теореме 1.6.2.)
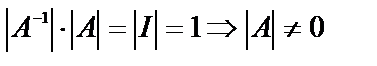
Достаточность: Пусть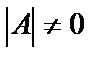 
Рассмотрим 
элементы С определяются как
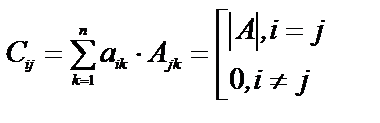
Пусть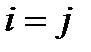 
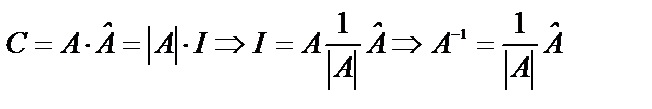
Получили способ нахождения обратимой матрицы , который используется только для матриц небольшого порядка.
Свойства обратных матриц:
1) (А-1) -1=А
2) (А×В)-1=В-1×А-1
3) I-1=I
