Второй алгоритм, использующий кратчайшие покрывающие деревья с минимальной длиной ребер на взвешенных графах - это алгоритм Краскала. Он содержит два шага.
1. Образуется "очередь" из всех ребер исходного графа, причем так, что ребра должны быть упорядочены по возрастанию весов или убыванию их в зависимости от поставленной задачи.
В нашем случае упорядочение идет по возрастанию весов.
n=5, значит количество ребер - 4.
Список ребер:
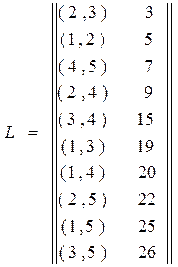
2. Выбираем из очереди первое, а затем следующие ребра с минимальным весом и вносим их в список Т' только в том случае, если внесение этого ребра в Т' не приводит к образованию цикла. Этот шаг повторяется до тех пор, пока в списке Т' не окажется (n-1) ребер, которые и образуют искомое МОД (минимальное основное дерево).
Т'
(2,3) 3 Выбирать следующие ребра не имеет смысла, так как
(1,2) 5 есть уже (n-1) = 4 ребро и последующие образуют цикл
(4,5) 7 с предыдущими.
(2.4) 9
Искомое МОД (минимальное основное дерево)

 5
5
9 3

Планарность графа.