Рассмотрим алгоритм Хелда и Карпа.

1. Строятся все кратчайшие пути, соединяющие X1 с любой вершиной L(L=2,3,...n). Длина любого из них равна расстоянию d_1,L от X1 до ХL.

2. Определяются путь минимальной длины, соединяющий X1 и ХL и проходящий через одну промежуточную вершину Х_m.

Зная длину минимального пути из X1 в XL с одной промежуточной вершиной, можно определить длину пути минимальной длины между X1 и XL, проходящего через 2-е промежуточные вершины, через 3 и т.д. При известном числе промежуточных вершин обязательно будет построен путь минимальной длины из X1 в любую вершину, проходящий через все остальные вершины. Тогда можно определить минимальный путь с учетом возвращения в X1.

Пример 1.Пусть граф G задан матрицей расстояния.

10

1 8 5

2

1. Согласно алгоритму определяется пути ведущие из X1 в XL (L=2,3).

Длина пути определяется весом ребер.

Из матрицы D d_1,2 = 10,

d_1,3 = 8.

2. Находим пути минимальной длины, соединяющие X1 с Х2 и проходящие через промежуточные вершины.

d³_1,2 = d_1,3 + d₃,₂ = 8 + 2 = 10,

d²_1,3 = d₁,₂ + d₂,₃ = 10 + 20 = 30.

3. Определим минимальную длину пути, включая возвращение в X1.

d³_1,2,1 = d³_1,2 + d₂,₁ = 10 + 5 = 15 — min X1 → Х3 → X2 → X1

d²_1,3,1 = d²_1,3 + d₃,₁ = 30 + l = 31.

Пример 2.

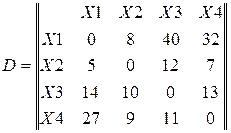
1. d_1,2 = 8

d_1,3 = 40

d_1,4 = 32

2.

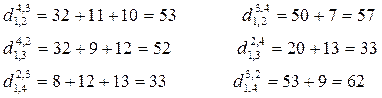
3. С возвращением в X1.

d_1,4,2,3,1 = 53 + 14 = 67 d_1,3,2,4,1 = 57 + 27 = 84

d_1,4,3,2,1 = 53 + 5 = 58 d_1,2,3,4,1 = 33 + 27 = 60

d_1,2,4,3,1 = 26 + 14 = 40 d_1,3,4,2,1 = 62 + 5 = 67