Теорема: Если векторы  и
и  заданы своими координатами:
заданы своими координатами:  = {Х1;У1; Z1},
= {Х1;У1; Z1}, 
 = {Х2;У2; Z2}, то их скалярное произведение определяется формулой
= {Х2;У2; Z2}, то их скалярное произведение определяется формулой 

 = Х1
= Х1  Х2 +У1
Х2 +У1  У2+Z1
У2+Z1  Z2 .
Z2 .
Доказательство:Разложим векторы  и
и  по базису
по базису  ,
,  ,
, 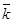 :
:  =Х1
=Х1  + У1
+ У1  + Z1
+ Z1 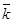 ,
, 
 = Х2
= Х2  + У2
+ У2  + Z2
+ Z2 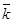 . Используя замечание (1), получаем:
. Используя замечание (1), получаем:


 = Х1
= Х1  Х2
Х2  2+Х1
2+Х1  У2
У2 
 +Х1
+Х1  Z2
Z2 
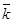 +У1
+У1  Х2
Х2 
 +У1
+У1  У2
У2  2 + У1
2 + У1  Z2
Z2 
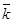 + Z1
+ Z1  Х2
Х2 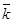
 + Z1
+ Z1  У2
У2 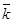
 + Z1
+ Z1  Z2
Z2 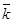 2.
2.
Откуда, используя равенства (2), находим: 

 =Х1
=Х1  Х2+У1
Х2+У1  У2+Z1
У2+Z1  Z2. g
Z2. g
Из теоремы вытекают два важных следствия.
Следствие 1: Необходимым и достаточным условием перпендикулярности векторов 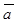 ={Х1;У1; Z1}, и
={Х1;У1; Z1}, и  = {Х2;У2; Z2} является равенство: Х1
= {Х2;У2; Z2} является равенство: Х1  Х2 +У1
Х2 +У1  У2+Z1
У2+Z1  Z2=0.
Z2=0.
Следствие 2: Угол между векторами  = {Х 1;У; Z 1},
= {Х 1;У; Z 1}, 
 = {Х2;У2; Z2} определяется равенством:
= {Х2;У2; Z2} определяется равенством:
Cos φ= 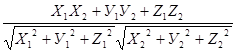
Действительно, по определению скалярного произведения 

 = ½
= ½  ½½
½½  ½ cos j, где j - угол, откуда cos j =
½ cos j, где j - угол, откуда cos j =  . Пример: Даны три точки А (1;1 1), В (2; 1;2), С (2 ;1; 2). Найти угол j= Ð ВАС.
. Пример: Даны три точки А (1;1 1), В (2; 1;2), С (2 ;1; 2). Найти угол j= Ð ВАС.
Решение. Применяя терему доказанную выше, найдем 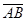 = {1 ;1;0;},
= {1 ;1;0;}, 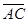 = {1;0;1}. Отсюда на основании следствия (2) получаем: cosj =
= {1;0;1}. Отсюда на основании следствия (2) получаем: cosj = 
 =
=  .
.
Следовательно, j = 600.