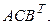Будем и в дальнейшем номера базисных векторов обозначать нижними индексами, а номера координат – верхними. Если задана совокупность чисел, снабженная двумя индексами, то договоримся располагать их в матрицу следующим образом: если оба индекса верхние или оба нижние, то первый будем считать номером строки, а второй – номером столбца, если один верхний, а один нижний, то номером строки будем считать верхний индекс. Кроме того, примем соглашение Эйнштейна: если в некотором произведении один и тот же индекс встречается дважды – снизу и сверху – то по нему проводится суммирование, ни один из индексов в произведении не должен встречаться более двух раз. При такой договоренности знак суммирования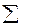 
в записи суммы опускается, а область изменения индекса суммирования понимается из контекста либо указывается дополнительно. Так, например, запись 
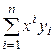заменяется просто на запись 
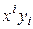. Если 
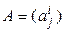и 
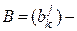квадратные матрицы
n-го порядка,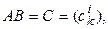 
то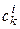 
запишется так: 
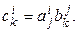Если же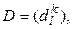 
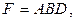то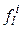 
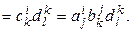Таким образом, в произведении элементы матриц-сомножителей располагаются по правилу цепочки: номер строки элемента каждой матрицы совпадает с номером столбца элемента матрицы предыдущей. Часто приходится по произведению элементов восстанавливать, произведению каких матриц оно принадлежит. Для этого элементы в произведении располагаем опять же по правилу цепочки. Так, например, 
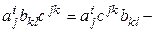элемент произведения ACB, а 
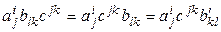– элемент 
