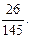Якщо відомі координати векторів 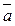 та
та 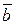 , то
, то
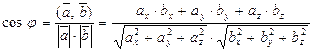 (22)
(22)
Приклад 9.Обчислити ( 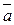 ,
, 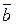 ), якщо
), якщо 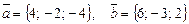 .
.
Розв’язання:
Користуючись формулою (21) знаходимо
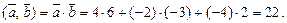
Відповідь: 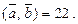
Приклад 10.При якому значенні m вектори 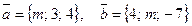 будуть перпендикулярними?
будуть перпендикулярними?
Розв’язання:
Два вектори перпендикулярні, якщо скалярний добуток дорівнює нулеві, тобто користуючись формулою (21) знаходимо скалярний добуток векторів тобто 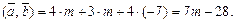 Оскільки вектори
Оскільки вектори 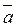 та
та 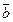 перпендикулярні, то
перпендикулярні, то 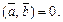 Отже,
Отже, 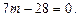 Звідси отримаємо, що
Звідси отримаємо, що 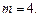
Відповідь:При 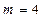 вектори
вектори 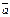 і
і 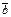 перпендикулярні.
перпендикулярні.
Приклад 11.Обчислити роботу, яку виконує сила 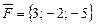 , коли її точка прикладання рухається прямолінійно, переміщуючись із положення А(2; -3; 5) в положення В(3; -2; -1).
, коли її точка прикладання рухається прямолінійно, переміщуючись із положення А(2; -3; 5) в положення В(3; -2; -1).
Розв’язання:
Згідно з формулою (20) робота 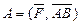 . Вектор переміщення
. Вектор переміщення 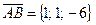 .
.
Тоді 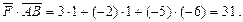
Відповідь:робота дорівнює 31од.
Приклад 12. Точки А(-1; 2; 4), В(-4; -2; 0), С(3; -2; 1) є вершинами ΔАВС. Знайти його внутрішній кут при вершині В.
Розв’язання:
Кут φ – це кут між векторами 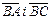
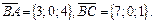 Тоді використовуючи формулу (22) отримаємо:
Тоді використовуючи формулу (22) отримаємо:
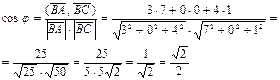
Отже, φ=450.
Відповідь:Кут при вершині В дорівнює 450.
Приклад 13. Дано вектори  Знайти проекцію вектора
Знайти проекцію вектора 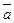 на вектор
на вектор 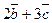 .
.
Розв’язання:
Користуючись формулою (19)
знаходимо 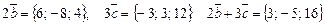 . Далі знаходимо скалярний добуток векторів
. Далі знаходимо скалярний добуток векторів 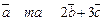 .
.
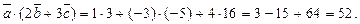
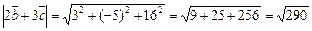
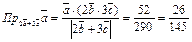 .
.
Відповідь:Проекція вектора 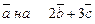 дорівнює
дорівнює