Определение. Любое конечное множество векторов  называется системой векторов.
называется системой векторов.
Определение. Выражение  , где
, где  называется линейной комбинацией системы векторов
называется линейной комбинацией системы векторов  , ачисла
, ачисла  называются коэффициентами этой линейной комбинации.
называются коэффициентами этой линейной комбинации.
Пусть L, Р и S – прямая, плоскость и пространство точексоответственно и  . Тогда
. Тогда  – векторные пространствавекторов как направленных отрезков на прямой L, на плоскости Р и впространстве S соответственно.
– векторные пространствавекторов как направленных отрезков на прямой L, на плоскости Р и впространстве S соответственно.
Определение. Базисом векторного пространства 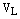 называется любой ненулевой вектор
называется любой ненулевой вектор 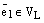 , т.е. любой ненулевой вектор коллинеарныйпрямой L:
, т.е. любой ненулевой вектор коллинеарныйпрямой L:  и
и  .
.
Обозначение базиса 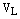 :
:  – базис
– базис 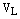 .
.
Определение. Базисом векторного пространства  называется любая упорядоченная пара неколлинеарных векторов пространства
называется любая упорядоченная пара неколлинеарных векторов пространства  .
.
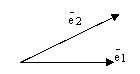
рис.1.
 , где
, где  ,
,  – базис
– базис  .
.
Определение. Базисом векторного пространства  называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства
называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства  .
.
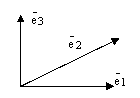
рис.2.
 – базис
– базис  .
.
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве 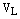 по определению, в пространстве
по определению, в пространстве  двавектора будут коллинеарные, если хотя бы один из них нулевой, впространстве
двавектора будут коллинеарные, если хотя бы один из них нулевой, впространстве  три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.
три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.