Определение порядков фильтров Баттерворта и Чебышева

Для заданных значений А_max, А_min, ω_n(нормированной частоты полосы непропускания f_д/2 деленной на f_в), для фильтра Баттерворта:

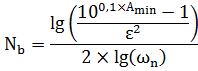
где

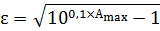
N_b присваивается целое значение, но не меньше расчетного, а для фильтра Чебышева:

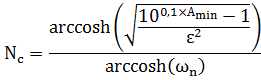
- для фильтра, имеющего наименьший порядок рассчитывается зависимость τ(ω) и строятся две зависимости на одном графике:

для фильтра Баттерворта:

τ_d:=Ψ(ω) и τ_b:=Ψ₁(ω),

а для фильтра Чебышева:

τ_d:= ψ(ω) и τ_с:= ψ₁(ω),

где ω нормированная относительно f_в частота (f/f_в)

τ_d строится по данным таблицы 2 путем кусочно-линейной или сплайн интерполяции (в среде MathCAD), с учетом того, что ω в таблице 2 в кГц равна f/10, где f – текущая частота в Гц;

- если для всех частот, приведенных в таблице 2

τ_d ≥ τ_с или τ_d ≥ τ_b,

то фильтр удовлетворяет всем требованиям поставленной задачи. В противном случае необходимо произвести проверку по τ(ω) для другого типа фильтра (у которого порядок выше). Если и у него не удовлетворяются требования по групповой задержке, то можно сделать вывод, что при заданных значениях А_max, А_min и ω_n данные фильтры не могут удовлетворять требованиям стандартов по групповому запаздыванию сигнала и следует руководствоваться указаниями пункта д) раздела 3.