Предположим имеем невесомую сис-му на которую с высоты h падает груз F. Под действ.падающего груза произойдет динамическая деформация:
Кинетическая энергия падающего груза= работе совершенной этим грузом:
T=F(h+∆д)
Потенциальная энергия упругой деформации равна:
U=F*∆cт/2
∆ст=(F*l)/(E*A)=F/(E*A/l)=F/c
c=E*A/l
U=(F/2)*(F/c)*(c/c)=(∆ст*с)/2
с – коэффиц. жесткости
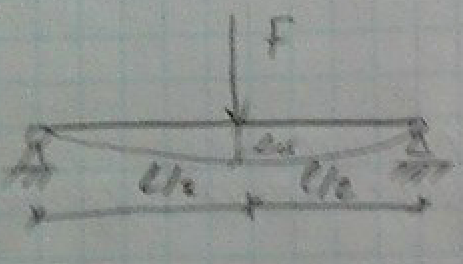
Коэф-нт жесткости «с» величина постоянная, зависит от упругих св-в материала и размеров. Покажем коэф-нт жесткости при изгибе:
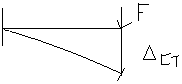
∆ст=(F*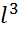 
)/3*E*I, (из справочника)
∆ст=F/(3*E*I/ 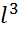)=F/c
C=3*E*I/
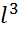
2
∆cт=(F* 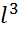)/48*E*I=F/c
C=48*E*I/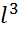
Т.о. величина с всегда известна
Приударных нагрузках деформации происходят такие же как и при статическом нагружении, но быстрее:
= 
*с/2
c=F/∆ст => = 
*F/2∆cт
приравняем кинетическую и потенциальную энергию при ударе:
F(h+∆д)= *F/2∆cт
2∆cт*h+2∆cт*∆д=
-2∆cт-∆cт*h=0
Получим квадратное ур-е, его решение имеет вид:
∆д=∆cт+-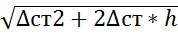 
знак – не рассматриваем т.к.ист. не имеет физический смысл.
=1+ 
– динамический коэфф. без учета массы сис-мы
Динамический коэфф. можно представить в др виде, зная связь между скоростью и высотой падения:
=1+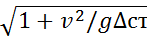 
Можно выразить его через энергию:
=1+ 
