Формулы, содержащие кроме переменных и скобок только знаки функции конъюнкции, дизъюнкции и отрицания(и, или, не), называются булевыми.
Теорема: Всякая логическая функция может быть представлена булевой формулой, т.е. как суперпозиция дизъюнкции, конъюнкции и отрицания.
Способ перехода от табличного задания логической функции к булевой формуле: для каждого набора значений переменных x1,x2,…,xn, на котором функция f(x1,x2,…,xn) равна 1, выписываются конъюнкции всех переменных: над теми переменными, которые на этом наборе равны 0, ставятся отрицания; все такие конъюнкции соединяются знаками дизъюнкции.
Полученная таким образом формула называется совершенной дизъюнктивной нормальной формой (СДНФ) логической функции f(x1,x2,…,xn).
Для каждой функции СДНФ единственна.
Пример:
Определить СДНФ операций:
x1→x2; x1 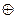 x2; x1 | x2
x2; x1 | x2
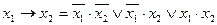
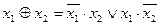
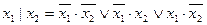
| x1
| x2
| x1→ x2
| x1 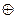 x2 x2
| x1 | x2
|
| 0
| 0
| 1
| 0
| 1
|
| 0
| 1
| 1
| 1
| 1
|
| 1
| 0
| 0
| 1
| 1
|
| 1
| 1
| 1
| 0
| 0
|