Решение:

Отношение R = {(a ,b): a+1=b или b+1=a}.

Это отношение антирефлексивно, симмитрично, не транзитивно.

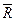
R																		R-1
	0	1	0	0	0	0				1	0	1	1	1	1				0	1	0	0	0	0
	1	0	1	0	0	0				0	1	0	1	1	1				1	0	1	0	0	0
	0	1	0	1	0	0				1	0	1	0	1	1				0	1	0	1	0	0
	0	0	1	0	1	0				1	1	0	1	0	1				0	0	1	0	1	0
	0	0	0	1	0	1				1	1	1	0	1	0				0	0	0	1	0	1
	0	0	0	0	1	0				1	1	1	1	0	1				0	0	0	0	1	0

Пример:

Пусть на множестве М = {1, 2, 3, 4, 5, 6} определено отношение R – “быть меньше ”. Задать матрицами отношение: R, 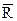, R^-1, R⁽²⁾,R⁰, R^*.

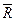
R																		R-1
	0	1	1	1	1	1				1	0	0	0	0	0				0	0	0	0	0	0
	0	0	1	1	1	1				1	1	0	0	0	0				1	0	0	0	0	0
	0	0	0	1	1	1				1	1	1	0	0	0				1	1	0	0	0	0
	0	0	0	0	1	1				1	1	1	1	0	0				1	1	1	0	0	0
	0	0	0	0	0	1				1	1	1	1	1	0				1	1	1	1	0	0
	0	0	0	0	0	0				1	1	1	1	1	1				1	1	1	1	1	0