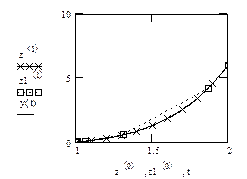Порядок виконання

1. Розв'язання рівняння методом Рунге-Кутта з постійним кроком за допомогою вбудованої функції rkfixed.

Права частина ОДУ:

f(x,y):=x²+2y

Початкова умова:

y₀:=0

Початок відрізка інтегрування:

a:=1

Кінець відрізка інтегрування:

b:=2

Кількість точок, у яких визначається розв'язок:

N:=10

Визначаємо наближені значення функції в заданих точках:

z:=rkfixed(y,a,b,N,f)

2. Розв'язання рівняння методом Рунге-Кутта з перемінним кроком за допомогою вбудованої функції rkadapt.

Точність розв'язку:

eps:=10^-3

Мінімальний припустимий крок розв'язання:

s:=0.01

Обчислення наближених значень функції:

z1:=rkadapt(y,a,b,eps,f,N,s)

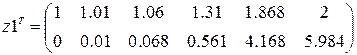
3. Розв'язання рівняння за допомогою вбудованої функції odesolve.

Given

=t²+2y(t)

y(1)=0

y:=odesolve(t,b,100)

t:=1,1.01..2

4. Графіки знайдених розв'язків ОДУ.