Понятие ранга матрицы тесно связано с понятием линейной зависимости и линейной независимости строк (столбцов) матрицы.
В матрице 
рассмотрим отдельные строки.
Обозначим строки 
; 
; …; 
.
Определение 1.16 Строка 
называется линейной комбинацией строк 
, если ее можно представить в виде
, где 
- числовые коэффициенты;
, 
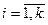
В этом случае, говорят, что строка линейно выражается через строки .
Определение 1.17 Система, состоящая из строкматрицы , называется линейно зависимой, если хотя бы одна из этих строк является линейной комбинацией других строк этой системы, например,
.
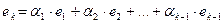В противном случае, если ни одна из строк не может быть представлена в виде линейной комбинации других строк этой системы, строки называются линейно независимыми.
Замечание. Следует отметить, что определение 1.17 не является строгим. Строгое определение линейно зависимой и линейно независимой системы будет дано ниже.
Примеры.
1) Рассмотрим строки 
и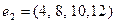 
. Нетрудно, заметить, что 
т. е. строка 
линейно выражается через строку 
, следовательно, строки 
- линейно зависимы.
