1. 
= 
. Это свойство вытекает из формулы числа сочетаний.
2. = 
+ 
.
3. 
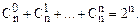
4. 
– бином Нютона. В частности, (х + у)2 = х2 + 2ху + у2; (х + у)3 = х3 + 3х2у + 3ху2 + у3 и т.д.
5. 
. Доказать легко с использованием бинома Ньютона на основе тождества (1 – 1)n = 0.
6. 
.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Определить наибольший коэффициент разложения 
, если сумма всех его коэффициентов равна 4096.
2. Найти наибольший член разложения 
.
3. Найти коэффициент при 
в разложении
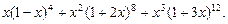
4. Определить число членов разложения 
.
5. Найти коэффициент при в разложении 
.
6. Найти коэффициент при 
в разложении 
.
7. Найти коэффициент при 
в разложении
.
8. Найти коэффициент при 
и 
в разложении 
.
9. В каком из выражений 
или 
будет наибольший коэффициент при .
10. Доказать, что: 
.
11. Вычислить суммы:
a) 
;
b) 
;
c) 
;
d) 
;
e) 
;
f) 
;
g) 
;
h) 
;
i) 
;
j) 
;
k) 
;
l) ;
m)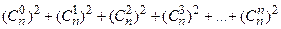 
n) 
.
12. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38, с ветчиной – 42, и с сыром и колбасой – 28, и с колбасой и ветчиной – 31, и с сыром и с ветчиной – 26. Все 3 вида бутербродов взяли 25 человек, а несколько человек захватили с собой пирожки. Сколько человек взяли с собой пирожки? Только бутерброды с ветчиной? Только два вида бутербродов?
13. Сколькими способами можно посадить за круглый стол 7 мужчин и 7 женщин так, чтобы никакие две женщины не сидели рядом?
