Задание 3.7. Используя таблицы значений, разложить данные функции в совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы:
а) f(x, y) = x Å y; г) f(x, y) = (x Ú y) ~ (x × y);
б) f(x, y) = x y; в) f(x, y, z) = y ~ (x Ú y×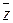 
);
в) f(x, y) = x | y; е) f(x, y, z) = (x × (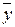 
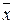®z)) ( 
| z).
Задание 3.8. Используя теорему о функциональной полноте, проверить, являются ли полными следующие системы, состоящие из одной функции:
а) f(x,y)= 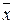× 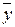; б) f(x,y,z) = 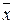×(y~z) Ú x×(yÅz).
