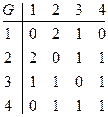Во многих задачах графы удобно задавать матрицами. Пусть граф G=(V, E) – граф c n вершинами и m ребрами, причем вершины и ребра занумерованы.
Матрицей инцидентности называется матрица A(G) размера m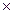 
n, элементы которой имеют вид
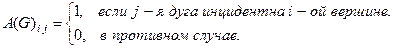
Матрицей смежности графа называется матрица B(G) n 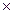n , которая имеет вид
B(G)i j =числу ребер, инцидентных одновременно i –той и j – ой вершинам.
П р и м е р .Задана матрица инцидентности графа (цифрами обозначены вершины, буквами – ребра графа).
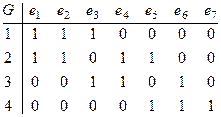
. Требуется:
a) Восстановить граф по матрице инцидентности;
b) Выяснить, является ли граф связным;
c) Построить для данного графа матрицу смежности
Р е ш е н и е .
2
a) e1 e5
1 e2 4
e4
e6
e3
3
h
Более компактным описанием графа по сравнению с матрицей инцидентности является список ребер.
Ребро e1 инцидентно вершинам 1 и 2.
Ребро e2 инцидентно вершинам 1 и 2.
Ребро e3 инцидентно вершинам 1 и 3.
Ребро e4 инцидентно вершинам 2 и 3.
Ребро e5 инцидентно вершинам 2 и 4
Ребро h инцидентно вершинам 4 и 4
b) .Граф является связным.
c) Матрица смежности имеет вид.
