Независимые множества

Независимое множество вершин – подмножество вершин графа G: SÍV такое, что любые две вершины в нем несмежны, то есть никакая пара вершин не соединена ребром.

подграф, порожденный независимым множеством–пустой граф.

Максимальное независимое множество –не является собственным подмножеством другого независимого множества.

Наибольшее независимое множество –наибольшее по мощности среди всех независимых множеств.

Число независимости a(G) графа G –мощность наибольшего независимого множества.

Например:

Максимальные независимые множества

; ; ;

; ;

; ;

.

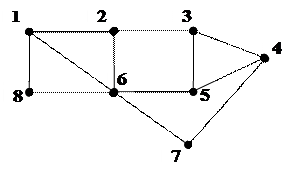
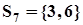Наибольшее независимое множество графа G: .

Число независимости графа G: a(G)=4.

Клика

Клика –подмножество вершин графа G такое, что любая пара из этого множества является смежной.

подграф, порожденный кликой – полный граф.

Максимальная клика –не является собственным подмножеством никакой другой клики графа G.

Наибольшая клика –наибольшая по мощности среди всех остальных клик графа G.

Кликовое число или плотность j(G) графа G –мощность наибольшей клики.

Например:

S₁={a,b,с};

S₂={b,d,e};

S₃={b,c,e};

S₄={b,d,c};

S₅={c,d,e};

S₆={b,c,d,e}.

Максимальные клики: S₁={a,b,с}, S₆={b,c,d,e}.

Наибольшая клика: S₆={b,c,d,e}.

Кликовое число: j(G)=4