Любая таблично заданная ФАЛ f(x1, x2, …, xn) (кроме тождественной единицы) может быть представлена в следующем аналитическом виде:
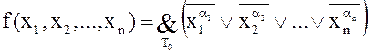
Представление ФАЛ в таком виде называется конъюнктивной совершенной нормальной формой этой функции (КСНФ).
Алгоритм построения конъюнктивной
совершенной нормальной формы
1. Выбрать в таблице все наборы аргументов, на которых функция обращается в 0.
2. Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом если аргумент xi входит в данный набор как 0, он вписывается без изменения в дизъюнкцию, соответствующую данному набору. Если xi входит в данный набор как 1, то в дизъюнкцию вписывается его отрицание.
3. Полученные дизъюнкции соединить операцией конъюнкция.
Например:
Построить ДСНФ и КСНФ для функции F(x,y,z).

Решение:
Для нахождения ДСНФ выбираем из таблицы №4 только те строки, в которых стоят наборы значений аргументов, обращающие функцию в единицу. Это вторая, третья и пятая строки. Выпишем конъюнкции, соответствующие выбранным строкам:
 .
.
Соединяя эти конъюнкции знаками дизъюнкции, получаем:
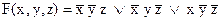 .
.
Для нахождения КСНФ выбираем из таблицы №4 только те строки, в которых стоят наборы значений аргументов, обращающие функцию в ноль. Выпишем соответствующие дизъюнкции и соединим их знаками конъюнкции.
Получим:  .
.