С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками.
Всякое сложное высказывание, которое, может быть получено из элементарных посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется формулой алгебры логики.
Формулы алгебры логики будем обозначать большими буквами латинского алфавита.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется ране, чем все остальные операции, дизъюнкция выполняется ранее, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
Например, формулы
(x&y)Úz и x→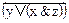 
могут быть записаны
x&yÚz и x→ 
.
Логические значений формул, полностью определяется логическими значениями входящих в нее элементарных высказываний. Например, если x = 1, y = 1, z = 0, то 
= 1.
Все возможные значения логические значения формулы могут быть описаны полностью с помощью таблицы истинности.
Например, для формулы x v y→x&y таблица истинности имеет вид:
