Утверждение 3. Пусть Д орграф, p(Д)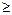 
2 – количество компонент сильной связности. Д1,…,Др – компоненты сильной связности. Тогда в результате удаления из Д вершин, содержащихся в Д1, получаем орграф с (р-1) компонентами сильной связности Д2,…,Др.
Утверждение 4. Пусть Д’ компонента сильной связности орграфа Д.
p(Д)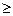 
2 и Д’’ орграф, полученный удалением из Д вершин, содержащихся в Д’. Тогда матрицы A(Д’’), S(Д’’) являются подматрицами матриц А(Д), S(Д), получаемыми в результате удаления из них строк и столбцов, соответствующих вершинам орграфа Д’.
Утверждение 5. Единицы i-ой строки или i-го столбца матрицы сильной связности орграфа Д=(V, X), V={v1,…,vn}, соответствуют вершинам компоненты сильной связности орграфа Д, содержащей вершину vi.
Из утверждений 3–5 следует алгоритм определения числа компонент сильной связности орграфа Д, а также матриц смежности этих компонент.
