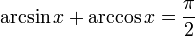Обратные тригонометрические функции
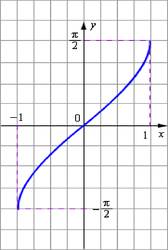 Аркcинус
Аркcинус
1. Определение
Арксинусом числа m называется такое значение угла х, для которого 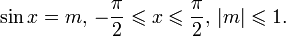
2. Свойства
- D (область определения по абсциссе) = [-1;1]
- E (область значения по ординате) = [- 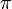 /2;
/2; 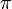 /2]
/2]
- Функция строго возрастает
- Нечетная функция: 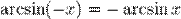
Арккосинус
1.  Определение
Определение
Арккосинусом числа m называется такое значение угла x, для которого 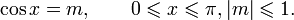
2.
cos ( 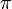 -arccos (x)= -cos (-arccos (x)) = = -cos(arccos (x)) = -x (По формуле приведения) -arccos (x)= -cos (-arccos (x)) = = -cos(arccos (x)) = -x (По формуле приведения)
| |
Свойства
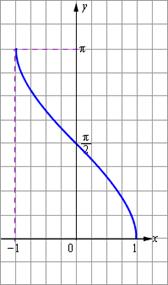
- D = [-1;1]
- E = [0; 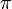 ]
]
- Функция строго убывает
- Функция центрально-симметрична относительно точки (0; 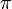 /2 ):
/2 ):
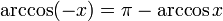
Док-во:
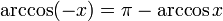
ßà
{cos ( 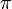 -arccos (x)= cos (arccos (-x)
-arccos (x)= cos (arccos (-x)
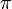 -arccos(x)
-arccos(x) 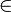 [0;
[0; 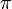 ]}
]}
ßà {cos (arccos (-x) = -x
arccos (x) 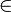 [0;
[0; 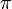 ]}
]}
* Многочлен Чебышёва: 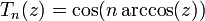
Основное соотношение: