Свойства:
1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е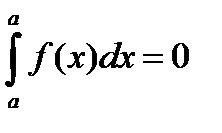 
2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
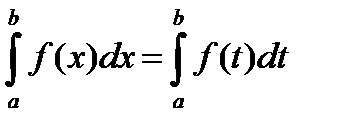
3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
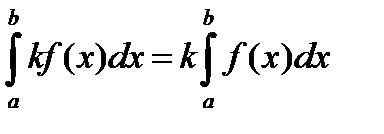
4. 
для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x)
5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если 
, то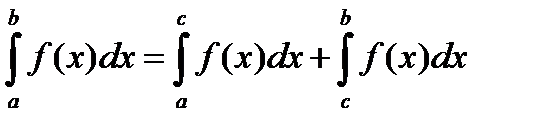 
6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
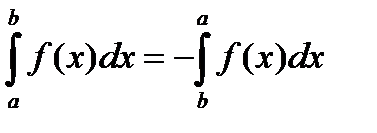
7. Если на отрезке [a;b] функции f(x) и g(x) интегрируемы и 
, то справедливо неравенство:
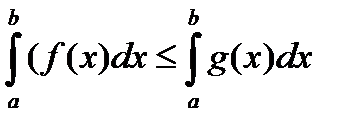
Теоремы об оценке интеграла.
1. Если на отрезке [a;b] выполняется неравенство 
, где m и M некоторые числа, то 
2. Если функция f(x) интегрируема по отрезку [a,b], то 
Теорема о среднем.
Если f(x) непрерывна на отрезке [a,b], то существует точка 
, такая что 
29. Замена переменной в определенном интеграле.
ТЕОРЕМА : Пусть функция 
непрерывна на отрезке 
.
Если:
1) функция 
и ее производная 
непрерывны при 
;
2) множеством значений функции 
при является отрезок ;
3) 
, 
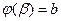, то справедлива формула
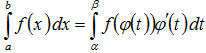
Эта формула носит название формулы замены переменной в определенном интеграле.
30. 
Интегрирование по частям в определенном интеграле
