|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Площадь и объем в полярных координатахДата добавления: 2015-06-12; просмотров: 3096; Нарушение авторских прав
|
|||||||||||||||||||||||||||||||||||||||||||||
Уроки php mysql Программирование
Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных

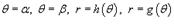 (рисунок 3). Тогда площадь этой области определяется формулой
(рисунок 3). Тогда площадь этой области определяется формулой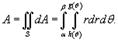
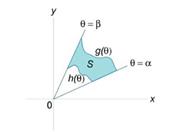
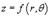 с основанием S, выражается в полярных координатах в виде
с основанием S, выражается в полярных координатах в виде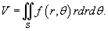
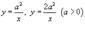 и вертикальными прямыми
и вертикальными прямыми 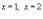 .
Решение.
Область R схематически показана на рисунке 4. Используя формулу для площади области I типа
.
Решение.
Область R схематически показана на рисунке 4. Используя формулу для площади области I типа
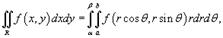 получаем
получаем
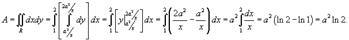
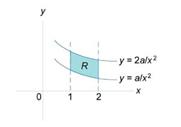
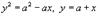 .
Решение.
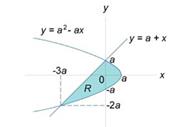
Сначала определим точки пересечения двух заданных линий.
.
Решение.
Сначала определим точки пересечения двух заданных линий.
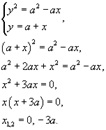 Следовательно, координаты точек пересечения равны
Следовательно, координаты точек пересечения равны
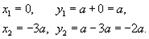 Область R представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
Область R представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
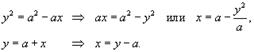 Получаем
Получаем
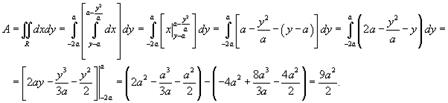
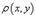 . Тогда масса пластины выражается через двойной интеграл в виде
. Тогда масса пластины выражается через двойной интеграл в виде
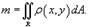 Статический момент пластины относительно оси Ox определяется формулой
Статический момент пластины относительно оси Ox определяется формулой
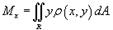 Аналогично находится статический момент пластины относительно оси Oy :
Аналогично находится статический момент пластины относительно оси Oy :
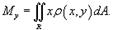 Координаты центра масс пластины, занимающей область R в плоскости Oxy с плотностью, распределенной по
закону
Координаты центра масс пластины, занимающей область R в плоскости Oxy с плотностью, распределенной по
закону 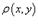 , описываются формулами
, описываются формулами
 Для однородной пластины с плотностью
Для однородной пластины с плотностью 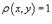 для всех (x, y) в области R центр масс определяется только формой
области и называется центроидом.
Моменты инерции пластины
Момент инерции пластины относительно оси Ox выражается формулой
для всех (x, y) в области R центр масс определяется только формой
области и называется центроидом.
Моменты инерции пластины
Момент инерции пластины относительно оси Ox выражается формулой
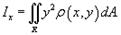 Аналогично вычисляется момент инерции пластины относительно оси Oy :
Аналогично вычисляется момент инерции пластины относительно оси Oy :
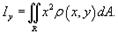 Полярный момент инерции пластины равен
Полярный момент инерции пластины равен
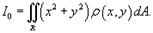 Заряд пластины
Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией
Заряд пластины
Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией 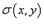 . Тогда полный заряд пластины Q определяется выражением
. Тогда полный заряд пластины Q определяется выражением
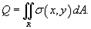 Среднее значение функции
Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть f (x,y)является непрерывной функцией в замкнутой области R в плоскости Oxy. Среднее значение функции μфункции f (x,y) в области R определяется формулой
Среднее значение функции
Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть f (x,y)является непрерывной функцией в замкнутой области R в плоскости Oxy. Среднее значение функции μфункции f (x,y) в области R определяется формулой
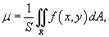 , где
, где 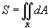 − площадь области интегрирования R.
− площадь области интегрирования R.
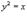 и
и  .
Решение.
Заданная пластина имеет форму, показанную на рисунке 1. Поскольку пластина однородна, то можно
положить
.
Решение.
Заданная пластина имеет форму, показанную на рисунке 1. Поскольку пластина однородна, то можно
положить 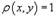 . Тогда масса пластины равна
. Тогда масса пластины равна
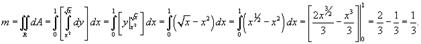 Найдем теперь статические моменты относительно осей Ox и Oy.
Найдем теперь статические моменты относительно осей Ox и Oy.
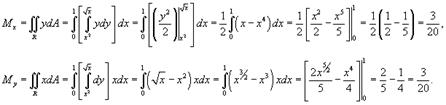 Вычисляем координаты центра масс.
Вычисляем координаты центра масс.
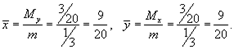
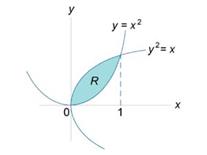

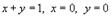 (рисунок 2) и имеющего плотность
(рисунок 2) и имеющего плотность 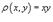 .
Решение.
Найдем момент инерции пластины относительно оси Ox.
.
Решение.
Найдем момент инерции пластины относительно оси Ox.
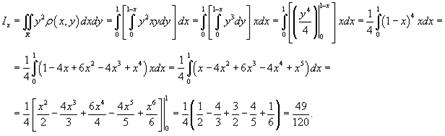 Аналогично вычислим момент инерции относительно оси Oy.
Аналогично вычислим момент инерции относительно оси Oy.
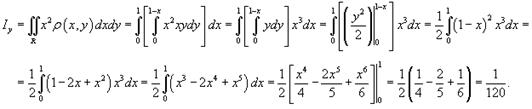
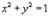 таким образом, что его поверхностная плотность равна
таким образом, что его поверхностная плотность равна 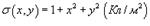 . Вычислить полный заряд диска.
Решение.
В полярных координатах область, занятая диском, описывается множеством
. Вычислить полный заряд диска.
Решение.
В полярных координатах область, занятая диском, описывается множеством 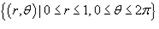 . Полный заряд будет равен
. Полный заряд будет равен