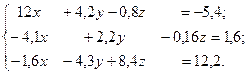Ввести матрицы
А = , B = , C =
и найти значение заданного выражения. Если результат не целочисленный, отобразить его в формате rat. Изучить информацию о переменных при помощи команды whos. Открыть окно для просмотра переменных рабочей среды Workspace. Заменить с использованием редактора Array Editor матрицы A, B, C на новые
А = , B = , C = ,
и повторить вычисления.
Варианты
1. (A3+CB)(A2+2CB)T 2. A4+3A2−ACB 3. BAC−5CTBT 4. 2BA-1C−BAC+3BC
5. -2CTAC−BBT 6. (BCB−2CT)A2 7. (ABT−C)(C+ABT)T 8. (ABTB)3BTCTA
9. CT(BTB+CCT)C 10. AAT−(CB)2+3(CB)-2 11. (BTB−3AT)A-2
12. (CBATC−C)(C+CBATC)T 13. (2CTAC−BBT)CT +B
14. 2C(BBT+CTC)CT+CB−A3 15. CB−(AAT)2+3CBA
Задание 3 (1.11). Решить систему линейных алгебраических уравнений
Дана система линейных алгебраических уравнений Ах = в. Вычислить определитель │А│. Если │А│ ≠ 0, решить систему с помощью оператора обратного деления < \ >.Проверить решение подстановкой. Вычислить обратную матрицу А-1 и решить систему с помощью с помощью обратной матрицы. Если полученное решение приближенное, повторить вычисления в формате rat.
Варианты
1.  2.
2.  3.
3. 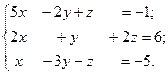
4.  5.
5.  6.
6. 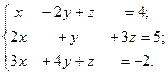
7.  8.
8.  9.
9. 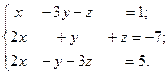
10.  11.
11. 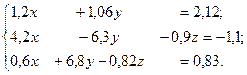
12.  13.
13. 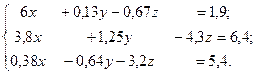
14.  15.
15.