Предполагает прохождение потока данных через последовательность функциональных блоков, реализующих операции над данными, при этом выполнение операций могут быть совмещено.
Классическим примером задачи является задача сложения векторов. Задачу можно решить организовав конвейер, в котором имеется четыре ci=bi+ai функциональных устройства: 1)для любой пары входных значений элементов векторов осуществляется сравнение порядков
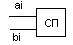
2)Осуществляет выравнивание порядков
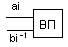
3)Сложение мантисс
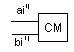
4)Организует нормализацию результатов
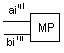
| Элемент
| СП
| ВП
| СМ
| НР
|
|
| a1b1
|
|
|
|
|
| a2b2
| a1b1
|
|
|
|
| a3b3
| a2b2
| a1b1
|
|
|
| a4b4
| a3b3
| a2b2
| a1b1
|
| ….
| ….
| …..
| ….
| ….
|
| N
| anbn
| an-1bn-1
| an-2bn-2
| an-3bn-3
|
| N+1
|
| anbn
| an-1bn-1
| an-2bn-2
|
| N+2
|
|
| anbn
| an-1bn-1
|
| N+3
|
|
|
| anbn
|
Без конвейеризации мы вычислили бы задачу по формуле: T1= nΣ(от k до i=1) ti, где к – количество операций, которое вычисляем, t – время, n- количество векторов.
Е2=(n+k-1)*m, где m- длительность самой продолжительной операции.