Разбиваем множество на части, границы которых кусочно-гладкие. Пусть функция ограничена на этом множестве. Величина - интегральная сумма. Переходя к пределу, получаем
интеграл на n-мерном множестве, имеющем n-мерный объём. Как обычно, интегрируемость означает:
.
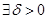
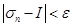
Свойства n-кратного интеграла те же, что у тройного.
, 
, 
.
.
- интегральная сумма. Переходя к пределу, получаем
.