«Неопределенный интеграл»
Проинтегрировать:
Блок 1)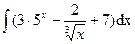 
; 
; 
; 
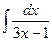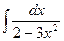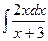– используем метод непосредственного интегрирования.
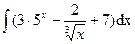
Решение.Используем свойство линейности неопределенного интеграла:
= 
.
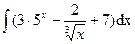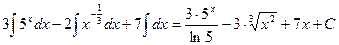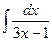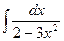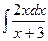; ; – «почти табличные» интегралы. Используем свойство инвариантности формулы интегрирования. Для сведения интеграла к табличному интегралу подводим линейную функцию под знак дифференциала.
.
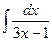Решение.Подведем линейную функцию 
под знак дифференциала и воспользуемся табличным интегралом 
: 
.
.
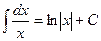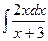Решение.Предварительно преобразуем подынтегральное выражение, подведем линейную функцию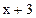 
под знак дифференциала и воспользуемся табличными интегралами 
и :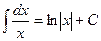
.
.
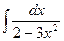Решение.Сведём данный интеграл к табличному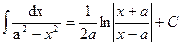 
:
.
Блок 2)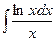 
; 
; 
; 
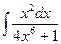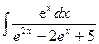– используем метод замены переменной.
