Итерационные методы решения систем линейных
Алгебраических уравнений
Метод простых итераций
Альтернативой точным методам решения систем линейных алгебраических уравнений являются итерационные методы, основанные на многократном уточнении 
– приближенно заданного решения системы 
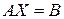. Верхним индексом в скобках здесь и далее по тексту обозначается номер итерации (совокупности повторяющихся действий).
Суть простейшего итерационного метода – метода простых итераций, состоит в выполнении следующих процедур.
1. Исходная система 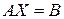преобразуется к равносильному виду:
, (2.1)
где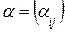 
– квадратная матрица, 
– вектор, 
. Это преобразование может быть выполнено различными путями, но для обеспечения сходимости итераций нужно добиться, чтобы норма матрицы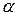 
была меньше единицы, то есть 
, где 
или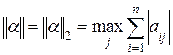 
.
2. Вектор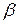 
принимается в качестве начального приближения 
и далее многократно выполняются действия по уточнению решения согласно рекуррентному соотношению
, 
(2.2)
или в развернутом виде
3. Итерации прерываются при выполнении условия
, (2.3)
где 
– заданная точность, которую необходимо достигнуть при решении задачи, или более простого условия
. (2.4)
