Пусть необходимо разложить рациональную функцию  ( – многочлены степеней
( – многочлены степеней  соответственно), являющуюся правильной рациональной дробью (
соответственно), являющуюся правильной рациональной дробью (  ), на сумму простейших дробей.
), на сумму простейших дробей.
Теорема (о разложении правильной рациональной дроби на простейшие дроби).Пусть знаменатель  правильной дроби (5.1) представлен в виде произведения линейных
правильной дроби (5.1) представлен в виде произведения линейных  и квадратичных
и квадратичных 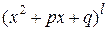 множителей (
множителей ( 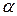 – есть
– есть  -кратный корень уравнения
-кратный корень уравнения  ,
,  ).
).
Тогда рациональную дробь (5.1) можно единственным образом представить в виде суммы простейших дробей:
при этом каждому множителю  в разложении знаменателя
в разложении знаменателя  на множители будет соответствовать сумма
на множители будет соответствовать сумма  -простейших дробей вида
-простейших дробей вида
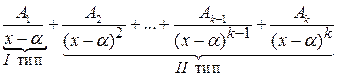 ,
,
а каждому множителю 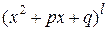 будет соответствовать сумма
будет соответствовать сумма 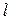 -простейших дробей вида
-простейших дробей вида
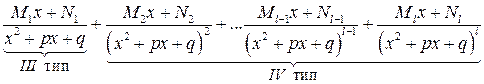 .
.
Теорема 5.1 показывает, какой вид будет иметь правильная рациональная дробь в разложении на простейшие дроби. Коэффициенты 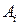 ,
,  ,
,  в разложении будем пока считать неопределенными.
в разложении будем пока считать неопределенными.
Пример. Разложить рациональную функцию
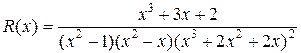
на простейшие дроби (коэффициенты разложения не вычислять).
Решение:Предварительно заметим, что данная функция является правильной рациональной дробью ( 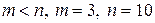 ). Разложим знаменатель
). Разложим знаменатель  =
=  на линейные
на линейные  и квадратичные
и квадратичные 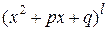 множители. Итак,
множители. Итак,  ,
, 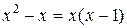 ,
,  . Таким образом,
. Таким образом,
 =
= 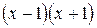

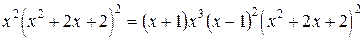 .
.
Тогда рациональную функцию  можно разложить на сумму простейших дробей следующим образом
можно разложить на сумму простейших дробей следующим образом
 =
=  ,
,
где 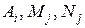 – некоторые постоянные (
– некоторые постоянные (  ,
,  ).
).