Дифференциальное уравнение такого звена имеет вид:
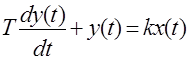
где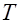 
– постоянная времени, с; 
– коэффициент усиления (передачи).
Передаточная функция
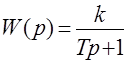, (2.15)
а переходная функция при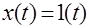 
.
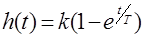При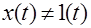 
.
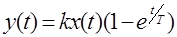2.5.2. Звенья второго порядка
Дифференциальные уравнения таких звеньев имеют вид
,
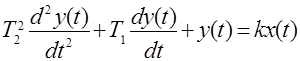а передаточная функция
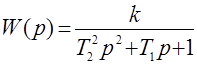(2.16)
В зависимости от соотношения постоянных времен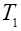и 
, и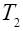 
звенья второго порядка подразделяются на апериодическое второго порядка и колебательные. В свою очередь колебательные звенья подразделяют на устойчиво колебательное (обычно его называют просто колебательным), консервативное и неустойчивое колебательное.
Соотношение 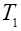, и 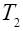выражают через коэффициент демпфирования 
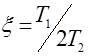. Обозначив 
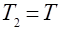, получим 
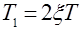и тогда (2.16) запишется в виде
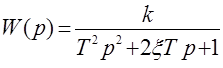(2.17)
Переходные процессы в звеньях второго порядка определяются видом корней характеристического уравнения.
