Метод ветвей и границ
Относится к группе комбинаторных методов дискретного программирования.
Центральная идея – полный перебор допустимого множества X заменяется частичным перебором.
В случае метода ветвей и границ это осуществляется путем разбиения дополнительного множества на подмножества (ветвления) и вычисления оценок (границ), позволяющих отбрасывать подмножества, заведомо не содержащее решение задачи.
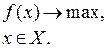(5.8)
X – конечное множество.
Основные принципы, лежащие в основе метода ветвей и границ:
1)вычисление верхней границы (оценки) f(x).
Пусть имеется множество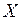 
или его подмножество
.
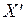Нужно найти верхнюю границу целевой функции на заданном множестве (подмножестве)
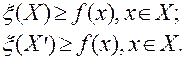
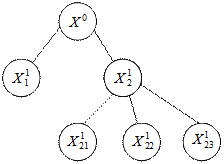
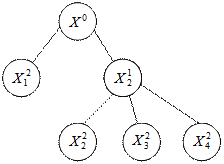
2)разбиение на подмножества (ветвления). Исходное множество X разбивается на отдельные подмножества, строится дерево подмножеств, которые как правило не пересекаются. Процедура пошаговая и реализуется следующим образом:
Шаг 0: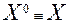
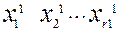
Шаг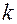 
: 
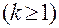
Числа имеющегося множества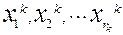 
, еще не подвергающиеся ветвлению. Из этих множеств выбирается некоторое множество 
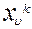, которое разбивается на подмножества 
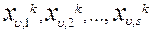. Множества 
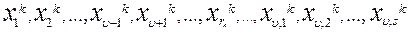переобозначаются в 
.
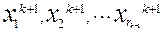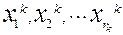
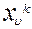
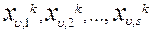
3)пересчет оценок.
Предполагается, что есть 
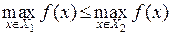
Поэтому, если :
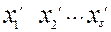
4)нахождение допустимых точек.
5)признак оптимальности.
Пусть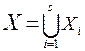 
и некоторая допустимая точка 
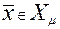. Если при этом 
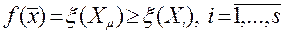,то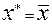 
.
