ЧИСЛЕННЫЕ МЕТОДЫ УСЛОВНЫХ ОПТИМИЗАЦИЙ.
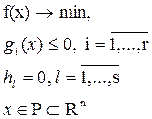 (4.1)
(4.1)
Если  – линейные функции и
– линейные функции и 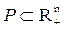 , то (4.1) – задача линейного программирования.
, то (4.1) – задача линейного программирования.
1)распространение аппарата линейного программирования на задачи нелинейного программирования путем использования последовательности процедур линейной аппроксимации
2)преобразование задачи условной оптимизации в эквивалентную ей последовательность задач безусловной оптимизации.
4.1. Метод аппроксимирующего программирования (МАП)
Применяется, когда выполняется условие 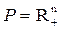 .
.
Метод аппроксимирующего программирования (МАП) представляет собой метод решения задач нелинейного программирования с помощью последовательности процедур линеаризации (линейной аппроксимации).
Все нелинейные функции в окрестности исследуемой точки заменяются линейными частями разложения в ряд Ньютона.
На k-итерации, используется точка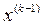 , чтобы определить
, чтобы определить  .
.
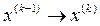
Задается начальная точка, определяемая методом перебора:
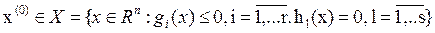
На k-итерации в окрестности точки 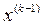 осуществляется линейная аппроксимация исходной задачи.
осуществляется линейная аппроксимация исходной задачи.
Считается, что все функции нелинейны.
Разложение имеет вид:
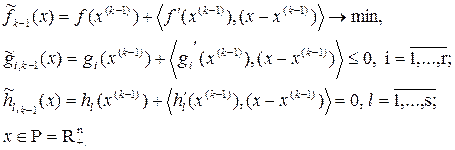
Задачу можно решить симплекс-методом. 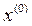 является решением задачи линейного программирования.
является решением задачи линейного программирования.
Зная точку 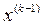 и
и 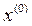 можно определить
можно определить 
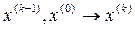
 должна удовлетворять условиям:
должна удовлетворять условиям:
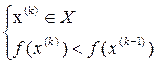 (4.2)
(4.2)
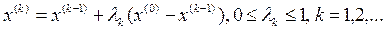 (4.3)
(4.3)
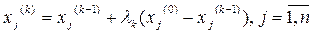 (4.4)
(4.4)
С помощью 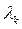 мы обеспечиваем выполнение условий (4.2)
мы обеспечиваем выполнение условий (4.2)
Начнем с 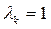 ,
, 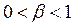 (максимальный шаг).
(максимальный шаг).
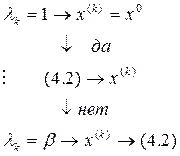
Графическая иллюстрация рассмотренных ситуаций.
1)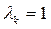
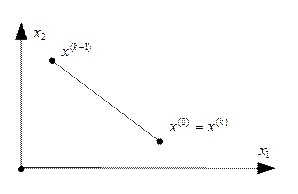
2)
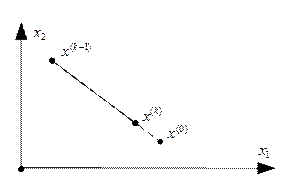
3) 
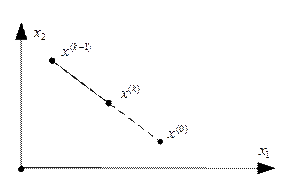
Условия окончания вычислений (1.44) и (1.45), но с относительной погрешностью.