Решение треугольной СЛАУ

Наиболее известным и популярным точным способом решения систем линейных алгебраических уравнений (СЛАУ) является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

первый элемент a₁₁⁽⁰⁾ не равен 0. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на a₁₁⁽⁰⁾ и исключим x₁ из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при x₁ в соответствующей строке. Получим

Если a₂₂⁽¹⁾, то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

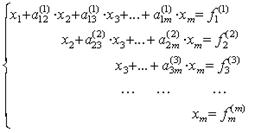
Из нее в обратном порядке находим все значения x_i:

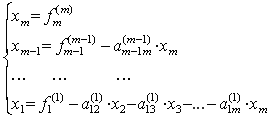
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных - обратным. Если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Тем не менее, для нормальной матрицы с ненулевым определителем всегда возможна такая перестановка уравнений, что на главной диагонали не будет нулей. В приведенном коде для простоты перестановок не делается, зато делается проверка решения, а прямой и обратный ход для наглядности вынесены в отдельные подпрограммы.