Площадь i-той элементарной трапеции можно оценить (приближенно вычислить) как площадь прямоугольника со сторонами 
и fi. Тогда 
и значение интеграла:
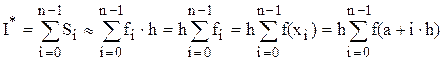
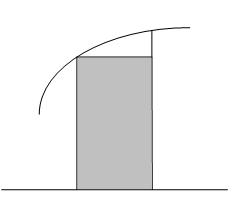
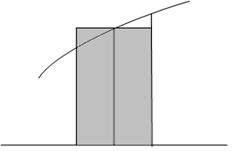
Оценка элементарной площади Si левым прямоугольником.
Полученная формула называется формулой левых прямоугольников, т.к. для оценки площади использовалось левое основание элементарной криволинейной трапеции.
Формула правых прямоугольников:
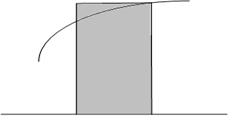
Оценка элементарной площади Si правым прямоугольником.
Для данного случая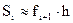 
и тогда значение интеграла:
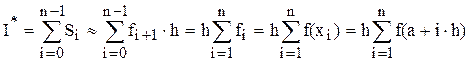
Эти формулы имеют большую погрешность, пропорциональную величине шага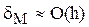 
Для повышения точности площадь Si можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка 
Для повышения точности площадь Si можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка
Оценка элементарной площади Si центральным прямоугольником.
Для данного случая 
и формула центральных прямоугольников имеет вид:
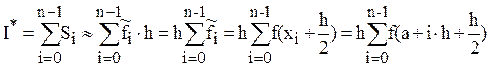
Погрешность в оценке площади Si в данном случае существенно меньше, чем в двух предыдущих (погрешность оценивается разницей площадей δ1 и δ2).
Погрешность метода пропорциональная квадрату величины шага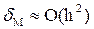 
Суммарная площадь
прямоугольников заметно
меньше площади
криволинейной трапеции.
