Результатом анализа марковской цепи являются ответы на два вопроса:
· как при известном начальном состоянии от шага к шагу меняются вероятности состояний, в которых может находиться система,
· каковы установившиеся значения этих вероятностей.
Покажем, как решается данная задача.
Имеем вектор-строку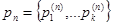 
.
В начальный момент времени состояние известно: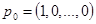 
.
Для расчета вероятностей используем уравнение Колмогорова-Чепмена:
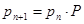, (1.7.1)
где Р - матрица вероятностей переходов.
С помощью уравнения Колмогорова-Чепмена можно вычислить вероятности состояний рекуррентно, т.е. последовательно:
,
,
,
…
.
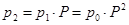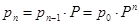При n→∞ можно определить установившиеся (финальные) вероятности. Для этого необходимо решить уравнение:
,
где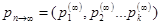 
.
Пример 1. Вероятностный автомат представлен в виде графа, изображенного на рисунке 1.7.2.
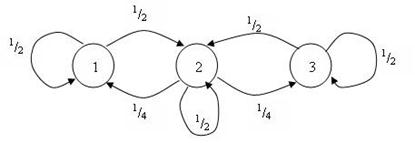
Рис. 1.7.2 Граф вероятностного автомата
Требуется определить, как меняется вектор вероятностей состояний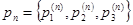 
, если 
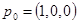и чему равны финальные вероятности.
Решение. На основе графа (рис. 1.7.2) составим матрицу вероятностей:
.
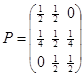Для определения векторов вероятностей состояний используем уравнение Колмогорова-Чепмена (1.7.1):
,
,
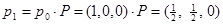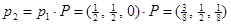и т.д.
Для определения финальных вероятностей составим уравнение:
.
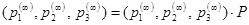Это уравнение равносильно системе уравнений:
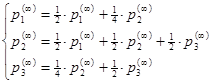
Для однозначного решения системы добавим нормирующую сумму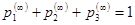 
. Тогда из второго уравнения следует, что 
.
Значения остальных вероятностей очевидны:
и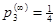 
.
