Сущность интегрирования методом трапеций составляет кусочно-линейная аппроксимация подынтегральной функции. Соседние точки (xi,yi) и (xi+1,yi+1), заданные таблицей в интервале a£x£b, соединяются прямыми. Если x0=a, а xn=b, то интеграл будет представлять собой сумму площадей n трапеций высотой h каждая. На рис. 15.3 показан графически принцип метода трапеций.

Рис.15.3. Интегрирование методом трапеций
Расчётная формула получается следующим образом:
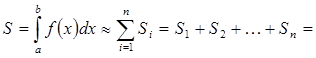
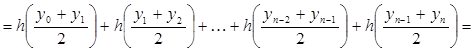
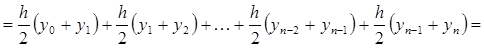
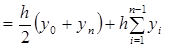
Итоговая формула выглядит следующим образом
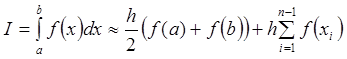
Таким образом, для вычисления определённого интеграла методом трапеций надо вычислить сумму значений подынтегральной функции в узлах интегрирования между a и b и умножить эту сумму на шаг интегрирования. К полученному значению прибавляется полусумма значений подынтегральной функции на концах отрезка, умноженная на шаг интегрирования. Совершенно очевидно, что чем меньше интервал h, через которые задаётся значение функции, тем с большей точностью будет вычислен определённый интеграл.