|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Алгоритм обучения рекуррентной сети ЭльманаДата добавления: 2014-11-28; просмотров: 776; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

 (6.26)
(6.26)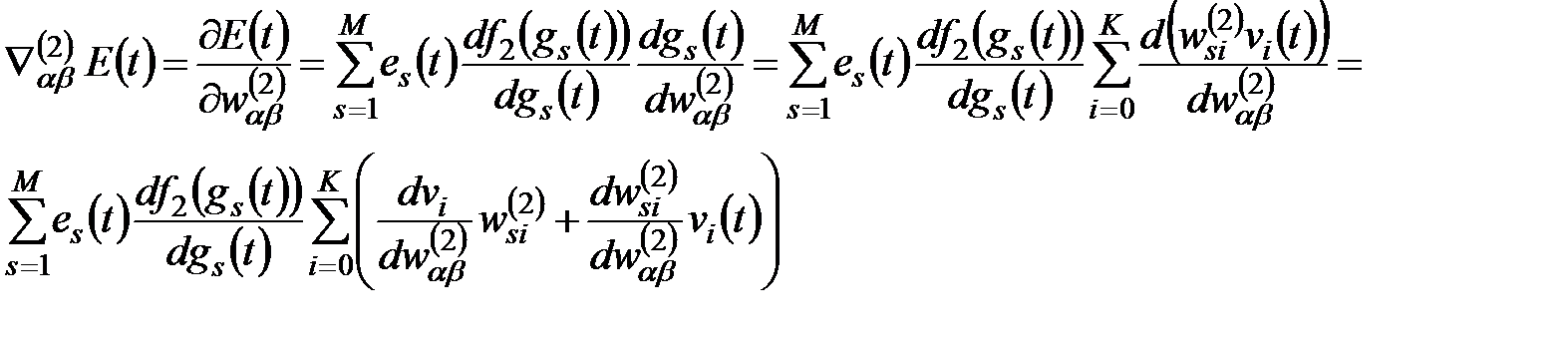 (6.27)
(6.27) (6.28)
(6.28) (6.29)
(6.29) уточняются по формуле:
уточняются по формуле: , (6.30)
, (6.30) (6.31)
(6.31)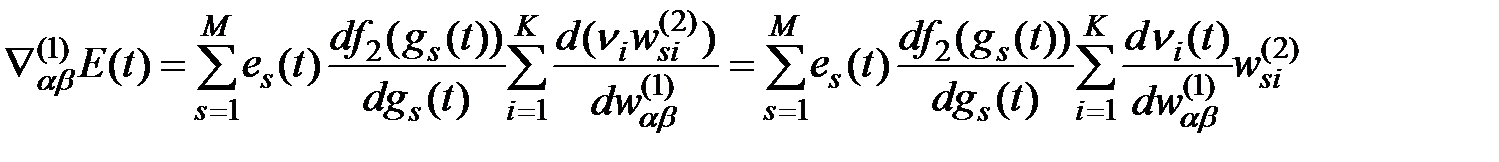 (6.32)
(6.32) (6.33)
(6.33) - дельта Кронекера, то есть:
- дельта Кронекера, то есть: .
. (формула (6.21)) в момент времени
(формула (6.21)) в момент времени  следует выражение (6.34):
следует выражение (6.34): . (6.34)
. (6.34) . Следует отметить, что это рекуррентная формула, определяющая производную в момент времени
. Следует отметить, что это рекуррентная формула, определяющая производную в момент времени  . Начальные значения производных в момент
. Начальные значения производных в момент  считаются нулевыми:
считаются нулевыми: . (6.35)
. (6.35) определить состояние всех нейронов сети (сигналы
определить состояние всех нейронов сети (сигналы  и
и  ). На этой основе можно сформировать входной вектор
). На этой основе можно сформировать входной вектор  для произвольного момента
для произвольного момента  .
. для нейронов выходного слоя как разность между фактическим и ожидаемым значениями сигналов выходных нейронов.
для нейронов выходного слоя как разность между фактическим и ожидаемым значениями сигналов выходных нейронов. (6.36)
(6.36) (6.37)
(6.37) .
. , (6.38)
, (6.38) - коэффициент момента, выбираемый из интервала (0, 1). Первое слагаемое этого выражения соответствует обычному методу обучения, второе – учитывает фактор момента, отражающий последнее изменение весов и не зависящий от фактического значения градиента. Чем больше величина
- коэффициент момента, выбираемый из интервала (0, 1). Первое слагаемое этого выражения соответствует обычному методу обучения, второе – учитывает фактор момента, отражающий последнее изменение весов и не зависящий от фактического значения градиента. Чем больше величина  , тем большее влияние на подбор весов оказывает слагаемое момента. Его значение существенно возрастает на плоских участках целевой функции и около локального минимума, где значение градиента близко к нулю.
, тем большее влияние на подбор весов оказывает слагаемое момента. Его значение существенно возрастает на плоских участках целевой функции и около локального минимума, где значение градиента близко к нулю.