Рис. 12 R-L-с цепочка
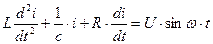
Пусть есть два процесса с параметрами:
1) {L1, R1, c1, t1, i1, U1, w1} = P1
2) {L2, R2, c2, t2, i2, U2, w2} = P2
По каждому из параметров введены определенные масштабные коэффициенты
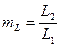 ,
, 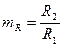 ,
, 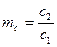 ,
, 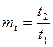 ,
, 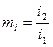 ,
, 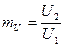 ,
, 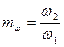 .
.
Воспользуемся ранее выведенными критериями, но по принципу размерности.
1) 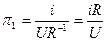
2) 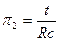
3) 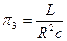
4) 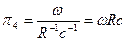 .
.
Группа независимых параметров [U, R,c].
Для 1-ой системы
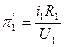 ,
, 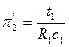 ,
, 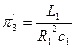 ,
, 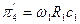 .
.
Для 2-ой системы с учетом масштабов:
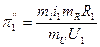 ,
, 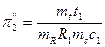 ,
, 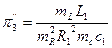 ,
, 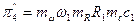 .
.
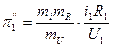 ,
, 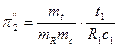 ,
, 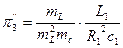 ,
, 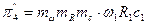 .
.
" pI = idem (все критерии одинаковы для подобных объектов)
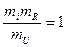 ,
, 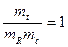 ,
, 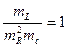 ,
, 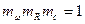 .
.
Эти уравнения называются масштабными уравнениями, при этом также существуют независимые масштабы (соответствующие независимым параметрам) mU, mR, mc , они выбираются произвольно.
Для данного примера имеем систему 4-го порядка с 4 неизвестными, но по p-теореме одно из этих уравнений является зависимым от других. В результате имеем систему 3-го порядка с 4-мя неизвестными. В общем случае решений такой системы может быть множество и выбрать одно единственное решение можно с помощью определенных ограничений, которые представляют собой условие однозначности.